pagerank
If we present nodes as pages and directed relationships between them as links, the PageRank algorithm outputs a probability distribution used to represent the likelihood that a person randomly clicking on links will arrive at any particular page.
PageRank theory holds that an imaginary surfer who is randomly clicking on links will eventually stop clicking. The probability, at any step, that the person will continue randomly clicking on links is called a damping factor, otherwise, the next page is chosen randomly among all pages.
PageRank is computed iteratively using the following formula:
Rank(n, t + 1) = (1 - d) / number_of_nodes
+ d * sum { Rank(in_neighbour_of_n, t) /
out_degree(in_neighbour_of_n)}Where Rank(n, t) is PageRank of node n at iteration t. In the end, rank
values are normalized to sum 1 to form a probability distribution.
The algorithm is implemented in such a way that all available threads are used to calculate PageRank, mostly for scalability purposes.
Default arguments are equal to default arguments in NetworkX PageRank implementation.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | directed |
| Edge weights | unweighted |
| Parallelism | parallel |
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
get()
The procedure calculates the PageRank.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
max_iterations: integer (default=100)➡ Maximum number of iterations within PageRank algorithm.damping_factor: double (default=0.85)➡ PageRanks damping factor. This is the probability of continuing the random walk from a random node within the graph.stop_epsilon: double (default=1e-5)➡ Value used to terminate the iterations of PageRank. If change from one iteration to another is lower than stop_epsilon, execution is stopped.num_of_threads: integer (default=1)➡ Number of threads used for executing the algorithm. Increasing the number of threads gives only marginal improvements so the recommended (and default) number of threads is 1.
Output:
node➡ Node in the graph, for which PageRank is calculated.rank➡ Normalized ranking of a node. Expresses the probability that a random surfer will finish in a certain node by a random walk.
Usage:
The following query calculated the PageRank:
CALL pagerank.get()
YIELD node, rank;Example
Database state
The database contains the following data:
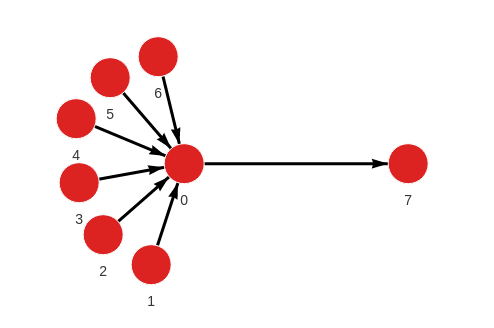
Created with the following Cypher queries:
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 7}) CREATE (a)-[:RELATION]->(b);Calculate PageRank
Calculate PageRank using the following query:
CALL pagerank.get()
YIELD node, rank
RETURN node, rank;Results:
+-----------------+-----------------+
| node | rank |
+-----------------+-----------------+
| (:Node {id: 1}) | 0.0546896 |
| (:Node {id: 0}) | 0.333607 |
| (:Node {id: 2}) | 0.0546896 |
| (:Node {id: 3}) | 0.0546896 |
| (:Node {id: 4}) | 0.0546896 |
| (:Node {id: 5}) | 0.0546896 |
| (:Node {id: 6}) | 0.0546896 |
| (:Node {id: 7}) | 0.338255 |
+-----------------+-----------------+