community_detection
Community in graphs mirrors real-world communities, like social circles. In a graph, communities are sets of nodes. M. Girvan and M. E. J. Newman note that nodes in a community connect more intensely with each other than with outside nodes.
This module employs the Louvain method for community detection based on Blondel’s paper Fast unfolding of communities in large networks using the Grappolo parallel approach.
Louvain’s algorithm is from the modularity maximization community detection family. It starts with each node in its own community, then uses a greedy approach to merge communities for the best modularity score. With an runtime for nodes, it suits large graphs. It’s further enhanced by parallelization via a distance-1 graph coloring and a coarsening technique preserving communities.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | undirected |
| Relationship weights | weighted / unweighted |
| Parallelism | parallel |
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
get()
Computes graph communities using the Louvain method.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
weight: string (default="weight")➡ Specifies the name of the edge property containing the edge weight. If the user doesn’t have a property to store weight on edges in their graph, the algorithm will set all weights to1, leading to the case of an unweighted graph. To utilize this algorithm for a weighted graph, edges need to have a property storing their weights. To have properties on edges, set--storage-properties-on-edgesflag toTruewhen starting Memgraph. Users can either use the default property nameweightor set another custom property name. If they set a custom property name for weight on edges, they need to provide that property name as a positional argument when calling the procedure. -
coloring: boolean (default=False)➡ If set, use the graph coloring heuristic for effective parallelization. -
min_graph_shrink: integer (default=100000)➡ The graph coarsening optimization stops upon shrinking the graph to this many nodes. -
community_alg_threshold: double (default=0.000001)➡ Controls how long the algorithm iterates. When the gain in modularity goes below the threshold, iteration is over. Valid values are between 0 and 1 (exclusive). -
coloring_alg_threshold: double (default=0.01)➡ If coloring is enabled, controls how long the algorithm iterates. When the gain in modularity goes below this threshold, a final iteration is performed using thecommunity_alg_thresholdvalue. Valid values are between 0 and 1 (exclusive). This parameter’s value should be higher thancommunity_alg_threshold. -
num_of_threads: integer (default=half of the system’s available hardware threads)➡ Specifies the number of threads used for parallel execution in the algorithm’s parallelized parts. Note: OpenMP (omp) is used for parallelization, so the actual thread usage may depend on system settings and OpenMP configurations.
Output:
node: Vertex➡ A graph node for which the algorithm was performed and returned as part of the results.community_id: integer➡ Community ID. Defaults to if the node does not belong to any community.
Usage:
Use the following query to detect communities:
CALL community_detection.get()
YIELD node, community_id;get_subgraph()
Computes graph communities over a subgraph using the Louvain method.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
subgraph_nodes: List[Node]➡ List of nodes in the subgraph. -
subgraph_relationships: List[Relationship]➡ List of relationships in the subgraph. -
weight: string (default=null)➡ Specifies the name of the property containing the edge weight. Users can set their own weight property; if this property is not specified, the algorithm uses theweightedge attribute by default. If neither is set, each edge’s weight defaults to1. To utilize a custom weight property, the user must set the--storage-properties-on-edges=trueflag. -
coloring: bool (default=False)➡ If set, use the graph coloring heuristic for effective parallelization. -
min_graph_shrink: int (default=100000)➡ The graph coarsening optimization stops upon shrinking the graph to this many nodes. -
community_alg_threshold: double (default=0.000001)➡ Controls how long the algorithm iterates. When the gain in modularity goes below the threshold, iteration is over. Valid values are between 0 and 1 (exclusive). -
coloring_alg_threshold: double (default=0.01)➡ If coloring is enabled, controls how long the algorithm iterates. When the gain in modularity goes below this threshold, a final iteration is performed using thecommunity_alg_thresholdvalue. Valid values are between 0 and 1 (exclusive). This parameter’s value should be higher thancommunity_alg_threshold.
Output:
node: Vertex➡ A graph node for which the algorithm was performed and returned as part of the results.community_id: int➡ Community ID. Defaults to if the node does not belong to any community.
Usage:
Use the following query to compute communities in a subgraph:
MATCH (a)-[e]-(b)
WITH COLLECT(a) AS nodes, COLLECT (e) AS relationships
CALL community_detection.get_subgraph(nodes, relationships)
YIELD node, community_id;Example
Database state
The database contains the following data:
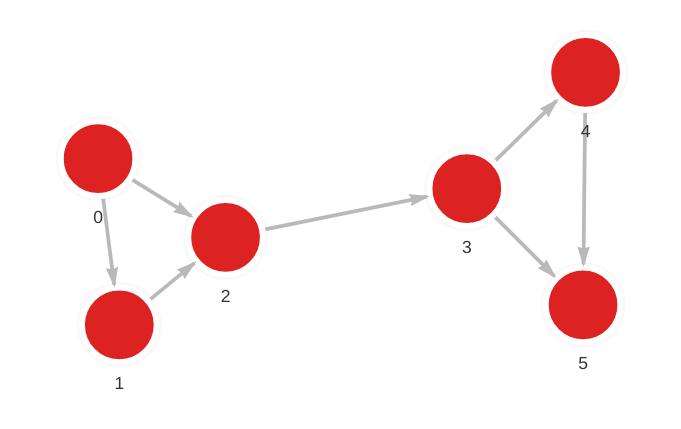
Created with the following Cypher queries:
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 1}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 1}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 2}) MERGE (b: Node {id: 3}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 4}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 4}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);Detect communities
Get communities using the following query:
CALL community_detection.get()
YIELD node, community_id
RETURN node.id AS node_id, community_id
ORDER BY node_id;Results show which nodes belong to community 1, and which to community 2:
┌─────────────────────────┬─────────────────────────┐
│ node_id │ community_id │
├─────────────────────────┼─────────────────────────┤
│ 0 │ 1 │
│ 1 │ 1 │
│ 2 │ 1 │
│ 3 │ 2 │
│ 4 │ 2 │
│ 5 │ 2 │
└─────────────────────────┴─────────────────────────┘