node2vec

The node2vec is a semi-supervised algorithmic framework for learning continuous feature representations for nodes in networks. The algorithm generates a mapping of nodes to a low-dimensional space of features that maximizes the likelihood of preserving network neighborhoods of nodes. By using a biased random walk procedure, it enables exploring diverse neighborhoods. In tasks such as multi-label classification and link prediction, node2vec shows great results. Check out Scalable Feature Learning for Networks (opens in a new tab) by A. Grover and J. Leskovec.

The node2vec algorithm was inspired by a similar NLP technique. The same way as a document is an ordered sequence of words, by sampling sequences of nodes from the underlying network and turning a network into an ordered sequence of nodes. Although the idea of sampling is easy, choosing the actual strategy can be challenging and dependant on the techniques that will be applied afterward.

Capturing information in networks often shuttles between two kinds of similarities: homophily and structural equivalence. Under the homophily hypothesis, nodes that are highly interconnected and belong to similar network clusters or communities should be embedded closely together. In contrast, under the structural equivalence hypothesis, nodes that have similar structural roles in networks should be embedded closely together (e.g., nodes that act as hubs of their corresponding communities).

The current implementation easily captures homophily or structural equivalence by changing hyperparameters.

BFS and DFS strategies play a key role in producing representations that reflect either of the above equivalences. The neighborhoods sampled by BFS lead to embeddings that correspond closely to structural equivalence. The opposite is true for DFS. It can explore larger parts of the network as it can move further away from the source node. Therefore, DFS sampled walks accurately reflect a macro-view of the neighborhood, which is essential in inferring communities based on homophily.

By having different parameters:

return parameter p
and in-out parameterq

one decides whether to prioritize the BFS or DFS strategy when sampling. If p is smaller than 1, then we create more BFS like walks and we capture more structural equivalence. The opposite is true if q is smaller than 1. Then we capture DFS like walks and homophily.

node2vec can be used for link prediction (opens in a new tab). We recommend you use the link prediction with GNN as it's more precise (node2vec gives a correct results in approximately 35% cases, while GNNs are correct in approximately 75% cases).

Source code

Trait	Value
Module type	module
Implementation	Python
Graph direction	directed/undirected
Edge weights	weighted/unweighted
Parallelism	sequential

Too slow?

If this algorithm implementation is too slow for your use case, open an issue on Memgraph's GitHub repository (opens in a new tab) and request a rewrite to C++!

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

`get_embeddings()`

The procedure returns calculated embeddings and the corresponding list of embeddings.

Input:

subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
is_directed : boolean ➡ If True, graph is treated as directed, otherwise it's treated as undirected
p : float ➡ Return hyperparameter for calculating transition probabilities.
q : float ➡ In-out hyperparameter for calculating transition probabilities.
num_walks : integer ➡ The number of walks per node in the walk sampling.
walk_length : integer ➡ Length of one walk in the walk sampling.
vector_size : integer ➡ Dimensionality of the word vectors.
alpha : float (default=0.025) ➡ The initial learning rate.
window : integer ➡ The maximum distance between the current and predicted word within a sentence.
min_count : integer ➡ Ignores all words with total frequency lower than this.
seed : integer ➡ Seed for the random number generator. Initial vectors for each word are seeded with a hash of the concatenation of word + str(seed).
workers : integer ➡ Use these many worker threads to train the model (=faster training with multicore machines).
min_alpha : float ➡ Learning rate will linearly drop to min_alpha as training progresses.
sg : {0, 1} ➡ Training algorithm: 1 for skip-gram; otherwise CBOW.
hs : {0, 1} ➡ If 1, hierarchical softmax will be used for model training. If 0, and negative is > 0, negative sampling will be used.
negative : integer ➡ If > 0, negative sampling will be used, the integer for negative specifies how many "noise words" should be drawn (usually between 5-20). If set to 0, no negative sampling is used. Either negative must be > 0 or hs must be set to 1.
epochs : integer (default=5)
edge_weight_property : string (default="weight")

Output:

nodes: mgp.List[mgp.Vertex] ➡ List of nodes for which embeddings were calculated
embeddings: mgp.List[mgp.List[mgp.Number]] ➡ Corresponding list of embeddings

Usage:

To get the calculated embeddings and the corresponding list of embeddings, use the following query:

CALL node2vec.get_embeddings(False, 2.0, 0.5, 4, 5, 100, 0.025, 5, 1, 1, 1, 0.0001, 1, 0, 5, 5, "weight");

`set_embeddings()`

The procedure calculates embeddings, creates a property of type List on a node with the embedding values and returns the corresponding list of embeddings.

Input:

subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
is_directed : boolean ➡ If True, graph is treated as directed, else not directed
p : float ➡ Return hyperparameter for calculating transition probabilities.
q : float ➡ In-out hyperparameter for calculating transition probabilities.
num_walks : integer ➡ The number of walks per node in walk sampling.
walk_length : integer ➡ Length of one walk in walk sampling.
vector_size : integer ➡ Dimensionality of the word vectors.
alpha : float ➡ The initial learning rate.
window : integer ➡ The maximum distance between the current and predicted word within a sentence.
min_count : integer ➡ Ignores all words with total frequency lower than this.
seed : integer ➡ Seed for the random number generator. Initial vectors for each word are seeded with a hash of the concatenation of word + str(seed).
workers : integer ➡ Use these many worker threads to train the model (=faster training with multicore machines).
min_alpha : float ➡ Learning rate will linearly drop to min_alpha as training progresses.
sg : {0, 1} ➡ Training algorithm: 1 for skip-gram; otherwise CBOW.
hs : {0, 1} ➡ If 1, hierarchical softmax will be used for model training. If 0, and negative is non-zero, negative sampling will be used.
negative : integer ➡ If > 0, negative sampling will be used, the int for negative specifies how many "noise words" should be drawn (usually between 5-20). If set to 0, no negative sampling is used.
epochs : integer (default=5)
edge_weight_property : string (default="weight")

Output:

nodes: mgp.List[mgp.Vertex] ➡ List of nodes for which embeddings were calculated
embeddings: mgp.List[mgp.List[mgp.Number]] ➡ Corresponding list of embeddings

Usage:

To calculate embeddings, use the following query:

CALL node2vec.set_embeddings(False, 2.0, 0.5, 4, 5, 100, 0.025, 5, 1, 1, 1, 0.0001, 1, 0, 5, 5, "weight");

`help()`

The procedure returns the list of available procedures and input parameters.

Output:

name: string ➡ Names of the available functions.
value: string ➡ Documentation for every function.

Usage:

To get help about the queries from this module, use the following query:

CALL node2vec.help()
YIELD name, value
RETURN name, value;

Example

Database state

The database contains the following data:

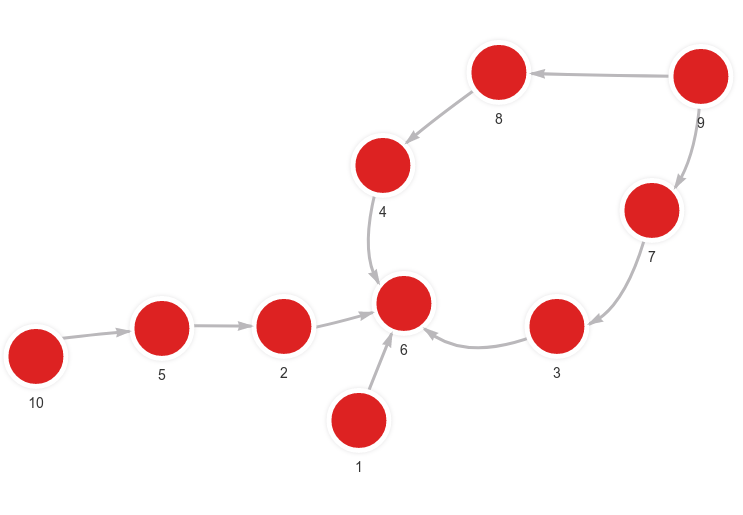
Input graph

Created with the following Cypher queries:

MERGE (n:Node {id: 1}) MERGE (m:Node {id: 6}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 2}) MERGE (m:Node {id: 6}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 10}) MERGE (m:Node {id: 5}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 5}) MERGE (m:Node {id: 2}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 9}) MERGE (m:Node {id: 7}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 7}) MERGE (m:Node {id: 3}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 3}) MERGE (m:Node {id: 6}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 9}) MERGE (m:Node {id: 8}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 8}) MERGE (m:Node {id: 4}) CREATE (n)-[:RELATION]->(m);
MERGE (n:Node {id: 4}) MERGE (m:Node {id: 6}) CREATE (n)-[:RELATION]->(m);

Set embeddings

Use the following query to set a new node property with the calculated embeddings:

CALL node2vec.set_embeddings(False, 2.0, 0.5, 4, 5, 2) 
YIELD nodes, embeddings
RETURN nodes, embeddings;

Check embeddings

Run the following query to check the embeddings:

MATCH (n)
RETURN n.id as node, n.embedding as embedding
ORDER BY n.id;

Result:

+-------------------------+-------------------------+
| node                    | embedding               |
+-------------------------+-------------------------+
| 1                       | [-0.243723, -0.0916009] |
| 2                       | [0.25442, 0.449585]     |
| 3                       | [0.322331, 0.448404]    |
| 4                       | [0.143389, 0.0492275]   |
| 5                       | [-0.465552, -0.35653]   |
| 6                       | [-0.0272922, 0.0111898] |
| 7                       | [0.368725, -0.0773199]  |
| 8                       | [-0.414683, -0.472285]  |
| 9                       | [-0.226683, 0.328159]   |
| 10                      | [-0.251244, -0.189218]  |
+-------------------------+-------------------------+