Advanced algorithmsAvailable algorithmsunion_find

union_find

Analysis of connected components is a common task in graph analytics.

By using a disjoint-set data structure that keeps track of them, the algorithm implemented in this module enables the user to quickly check whether a pair of given nodes is in the same or different connected component. A check on a pair of nodes is effectively executed in O(1) time.

The implementation of the disjoint-set data structure and its operations uses the union by rank and path splitting optimizations described in Robert E. Tarjan’s and Jan van Leeuwen’s “Worst-case Analysis of Set Union Algorithms” and presented with examples.

Source code
TraitValue
Module typemodule
ImplementationPython
Graph directionundirected
Edge weightsunweighted
Parallelismsequential

Too slow?

If this algorithm implementation is too slow for your use case, open an issue on Memgraph’s GitHub repository and request a rewrite to C++!

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

connected()

Use the procedure to check whether a pair of given nodes is in the same or different connected component.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • nodes1: Union[Vertex, List[Vertex]] ➡ First value (or list thereof) in connectedness calculation.

  • nodes2: Union[Vertex, List[Vertex]] ➡ Second value (or list thereof) in connectedness calculation.

  • mode: string (default="pairwise") ➡ Mode of combining nodes1 and nodes2. Can be p or pairwise for a pairwise product, or c or cartesian for a Cartesian product of the arguments. Pairwise by default.

  • update: boolean (default=True) ➡ Specifies whether the disjoint-set data structure should be reinitialized. Enabled by default. If the graph has been modified since the previous call of this procedure, turning update off ensures that the changes are not visible in the output.

Output:

  • node1: Vertex ➡ Node in nodes1.
  • node2: Vertex ➡ Node in nodes2.
  • connected: boolean ➡ True if the above nodes are in the same connected component of the graph.

Usage:

Analyze connected components using the following query:

MATCH (m:Node)
WITH collect(m) AS nodes1
MATCH (n:Node)
WITH collect(n) AS nodes2, nodes1
CALL union_find.connected(nodes1, nodes2) 
YIELD node1, node2, connected
RETURN node1, node2, connected;

Example

Database state

The database contains the following data:

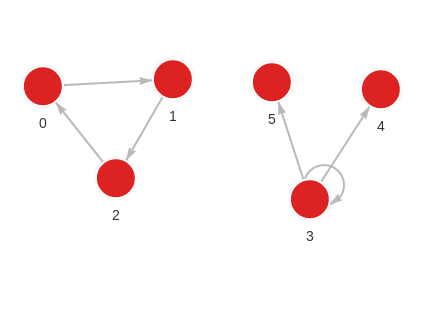
Created with the following Cypher queries:

MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);

Analyze connected components

Check whether a pair of given nodes is in the same or different connected component:

MATCH (m:Node)
WHERE m.id = 0 OR m.id = 1
WITH collect(m) AS nodes1
MATCH (n:Node)
WHERE n.id = 2 OR n.id = 3
WITH collect(n) AS nodes2, nodes1
CALL union_find.connected(nodes1, nodes2) 
YIELD node1, node2, connected
RETURN node1, node2, connected;

Results:

+-----------------+-----------------+-----------------+
| node1           | node2           | connected       |
+-----------------+-----------------+-----------------+
| (:Node {id: 0}) | (:Node {id: 2}) | false           |
| (:Node {id: 1}) | (:Node {id: 3}) | false           |
+-----------------+-----------------+-----------------+
tsputil_module