cycles
In graph theory, a cycle represents a path within the graph where only the starting and ending nodes are equal. Furthermore, cycles can be double-connected links between neighboring nodes or self-loops. The cycles detection algorithm implemented within MAGE works on an undirected graph and has no guarantee of node order in the output. The implemented algorithm (Gibb) is described in the 1982 MIT report called “Algorithmic approaches to circuit enumeration problems and applications” (Boon Chai Lee, 1982). The problem is not solvable in polynomial time. It is based on finding all subsets of fundamental cycles which takes about time where represents a set of relationships (edges) and represents a set of nodes (vertices) of the given graph.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | undirected |
| Edge weights | unweighted |
| Parallelism | sequential |
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
get()
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
Output:
cycle_id: integer➡ Incremental cycle ID of a certain node. There is no guarantee on how nodes are going to be ordered within cycle. The cycle can be represented with a minimum of one ID, where it stands for self-loop.node: Vertex➡ Vertex object with all properties which is going to be related to the cycle ID it belongs to.
Usage:
CALL cycles.get()
YIELD cycle_id, node;Example
Database state
The database contains the following data:
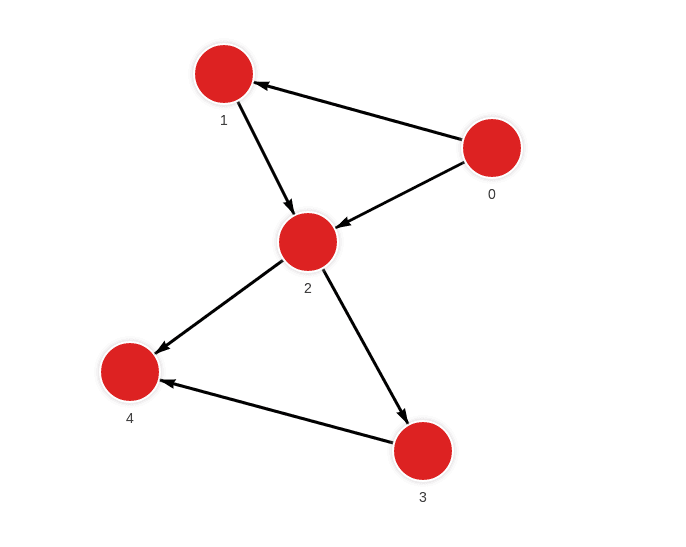
Created with the following Cypher queries:
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);Identify cycles
Get the values using the following query:
CALL cycles.get()
YIELD cycle_id, node
RETURN cycle_id, node;Results:
+-----------------+-----------------+
| cycle_id | node |
+-----------------+-----------------+
| 0 | (:Node {id: 2}) |
| 0 | (:Node {id: 0}) |
| 0 | (:Node {id: 1}) |
| 1 | (:Node {id: 4}) |
| 1 | (:Node {id: 2}) |
| 1 | (:Node {id: 3}) |
+-----------------+-----------------+