leiden_community_detection
Community in graphs mirrors real-world communities, like social circles. In a graph, communities are sets of nodes. M. Girvan and M. E. J. Newman note that nodes in a community connect more intensely with each other than with outside nodes.
This module employs the Leiden algorithm for community detection based on paper From Louvain to Leiden: guaranteeing well-connected communities. The Leiden algorithm is a hierarchical clustering algorithm, that recursively merges communities into single nodes by greedily optimizing the modularity and the process repeats in the condensed graph. It enhances the Louvain algorithm by addressing its limitations, particularly in situations where some identified communities are not well-connected. This improvement is made by periodically subdividing communities into smaller, well-connected groups. With an runtime for edges and number of iterations, it suits large graphs. The space complexity if for nodes and edges.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | undirected |
| Relationship weights | weighted / unweighted |
| Parallelism | parallel |
This implementation of Leiden is non-deterministic, meaning it can generate
different communities in subsequent runs. To control the randomness, tweak the
theta parameter.
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
get()
Computes graph communities using the Leiden algorithm. For more information on specific algorithm parameters and their use, refer to the paper From Louvain to Leiden: guaranteeing well-connected communities.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.weight_property: string (default="weight")➡ Specifies the name of the edge property containing the edge weight. If the user doesn’t have a property to store weight on edges in their graph, the algorithm will set all weights to1, leading to the case of an unweighted graph. To utilize this algorithm for a weighted graph, edges need to have a property storing their weights. To have properties on edges, set--storage-properties-on-edgesflag toTruewhen starting Memgraph. Users can either use the default property nameweightor set another custom property name. If they set a custom property name for weight on edges, they need to provide that property name as a positional argument when calling the procedure.gamma: double (default=1.0)➡ Resolution parameter used when computing the modularity. Higher resolutions lead to more smaller communities, while lower resolutions lead to fewer larger communities.theta: double (default=0.01)➡ Controls the randomness while breaking a community into smaller ones.resolution_parameter: double (default=0.01)➡ Minimum change in modularity that must be achieved when merging nodes within the same community.max_iterations: int (default=inf)➡ Maximum number of iterations the algorithm will perform. If set to infinity, the algorithm will run until convergence is reached.
Output:
node: Vertex➡ A graph node for which the algorithm was performed and returned as part of the results.community_id: integer➡ Community ID. Defaults to if the node does not belong to any community.communities: list➡ List representing the hierarchy of communities that a node has belonged to across iterations.
Usage:
Use the following query to detect communities:
CALL leiden_community_detection.get()
YIELD node, community_id, communities;The algorithm throws an exception if no communities are detected. This can happen if in the first iteration
all nodes merge into a single community or if each node forms its own. If this occurs, try adjusting the algorithm’s gamma parameter.
get_subgraph()
Computes graph communities over a subgraph using the Leiden method.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.subgraph_nodes: List[Node]➡ List of nodes in the subgraph.subgraph_relationships: List[Relationship]➡ List of relationships in the subgraph.weight: string (default=null)➡ Specifies the name of the property containing the edge weight. Users can set their own weight property; if this property is not specified, the algorithm uses theweightedge attribute by default. If neither is set, each edge’s weight defaults to1. To utilize a custom weight property, the user must set the--storage-properties-on-edges=trueflag.gamma: double (default=1.0)➡ Resolution parameter used when computing the modularity. Higher resolutions lead to more smaller communities, while lower resolutions lead to fewer larger communities.theta: double (default=0.01)➡ Controls the randomness while breaking a community into smaller ones.resolution_parameter: double (default=0.01)➡ Minimum change in modularity that must be achieved when merging nodes within the same community.max_iterations: int (default=inf)➡ Maximum number of iterations the algorithm will perform. If set to infinity, the algorithm will run until convergence is reached.
Output:
node: Vertex➡ A graph node for which the algorithm was performed and returned as part of the results.community_id: int➡ Community ID. Defaults to if the node does not belong to any community.communities: list➡ List representing the hierarchy of communities that a node has belonged to across iterations.
Usage:
Use the following query to compute communities in a subgraph:
MATCH (a)-[e]-(b)
WITH COLLECT(a) AS nodes, COLLECT (e) AS relationships
CALL leiden_community_detection.get_subgraph(nodes, relationships)
YIELD node, community_id, communities;Single Iteration Example
Database state
The database contains the following data:
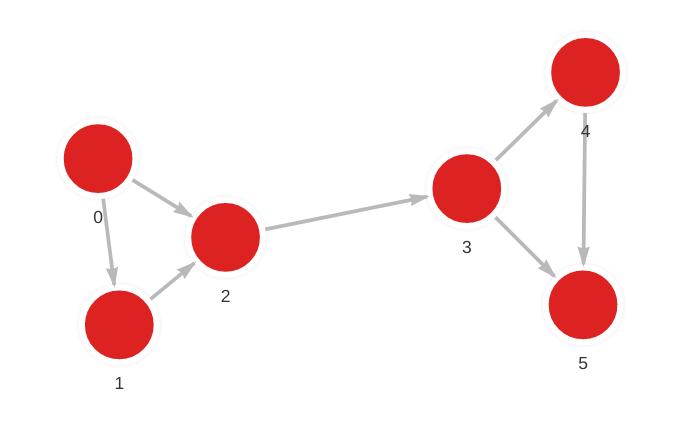
Created with the following Cypher queries:
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 1}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 0}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 1}) MERGE (b: Node {id: 2}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 2}) MERGE (b: Node {id: 3}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 4}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 3}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);
MERGE (a: Node {id: 4}) MERGE (b: Node {id: 5}) CREATE (a)-[r: Relation]->(b);Detect communities
Get communities using the following query:
CALL leiden_community_detection.get()
YIELD node, community_id, communities
RETURN node.id AS node_id, community_id, communities
ORDER BY node_id;Results show which nodes belong to community 0, and which to community 1.
+--------------+--------------+--------------+
| node_id | community_id | communities |
+--------------+--------------+--------------+
| 0 | 0 | [0] |
| 1 | 0 | [0] |
| 2 | 0 | [0] |
| 3 | 1 | [1] |
| 4 | 1 | [1] |
| 5 | 1 | [1] |
+--------------+--------------+--------------+Multiple Iterations Example
Database state
The database contains the following data:
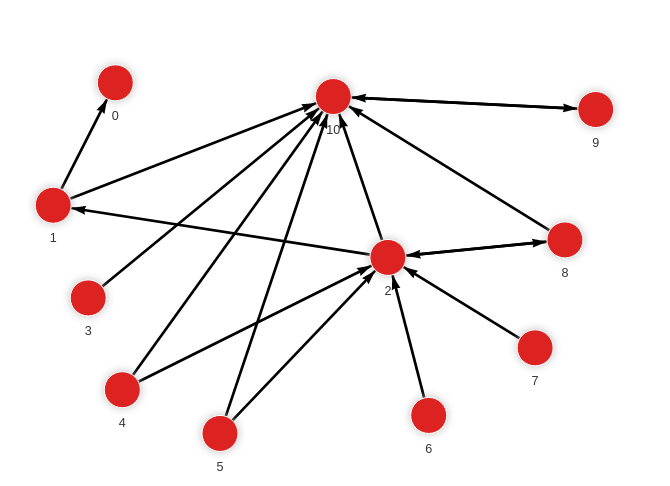
Created with the following Cypher queries:
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);Detect communities
Get communities using the following query:
CALL leiden_community_detection.get()
YIELD node, community_id, communities
RETURN node.id AS node_id, community_id, communities
ORDER BY node_id;The results show which nodes belong to community 0 and which to community 1, as well as how nodes changed communities across iterations.
+--------------+--------------+--------------+
| node_id | community_id | communities |
+--------------+--------------+--------------+
| 0 | 1 | [0, 1] |
| 1 | 1 | [0, 1] |
| 2 | 0 | [1, 0] |
| 3 | 1 | [2, 1] |
| 4 | 1 | [3, 1] |
| 5 | 0 | [4, 0] |
| 6 | 0 | [1, 0] |
| 7 | 0 | [1, 0] |
| 8 | 0 | [1, 0] |
| 9 | 1 | [2, 1] |
| 10 | 1 | [2, 1] |
+--------------+--------------+--------------+