degree_centrality

Degree centrality is the basic measurement of centrality that refers to the number of relationships adjacent to a node. For directed graphs, define an in-degree measure, which is defined as the number of in-coming edges, and an out-degree measure, defined as the number of out-going edges.

Let $A = (a_{i,j})$ be the adjacency matrix of a directed graph. The in-degree centrality $x_{i}$ of node $i$ is given by: $x_{i} = \sum_k a_{k,i}$ or in matrix form (1 is a vector with all components equal to unity): $x = 1 A$ . The out-degree centrality $y_{i}$ of node $i$ is given by: $y_{i} = \sum_k a_{i,k}$ or in matrix form: $y = A 1$ .

Source code

Trait	Value
Module type	algorithm
Implementation	C++
Graph direction	directed/undirected
Edge weights	unweighted
Parallelism	sequential

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

`get()`

The procedure calculates the degree centrality for each node in the graph.

Input:

type: string (default="undirected") ➡ Defines whether the procedure is using "in", "out", or "undirected" relationships.

Output:

node: Vertex ➡ Node in the graph, for which Degree Centrality is calculated.
degree: float ➡ Calculated degree of a node.

Usage:

The following query calculates the degree centralitry:

CALL degree_centrality.get()
YIELD node, degree;

`get_subgraph()`

The procedure calculates degree centrality for each node of the given subgraph.

Input:

nodes: list[node] ➡ Nodes that will be used in the algorithm.
relationships: list[relationship] ➡ Relationships that will be considered for degree calculation.
type: string (default="undirected") ➡ Defines whether the procedure is using "in", "out", or "undirected" relationships.

Output:

node: Vertex ➡ Node in the graph, for which degree centrality is calculated.
degree: float ➡ Calculated degree of a node.

Usage:

The following query calculates degree centrality on a subgraph:

MATCH (n:Person)
CALL degree_centrality.get()
YIELD node, degree;

Example

Database state

The database contains the following data:

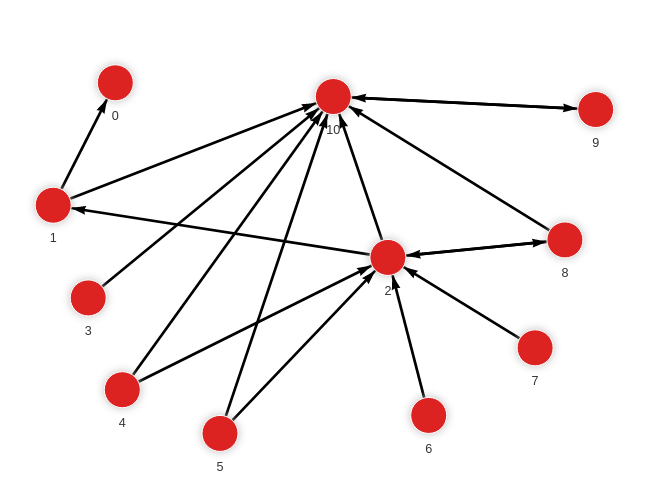
Created with the following Cypher queries:

MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);

Calculate centrality

Get the values using the following query:

CALL degree_centrality.get("in")
YIELD node, degree
RETURN node, degree;

Results:

+------------------+------------------+
| node             | degree           |
+------------------+------------------+
| (:Node {id: 1})  | 0.1              |
| (:Node {id: 0})  | 0.1              |
| (:Node {id: 10}) | 0.7              |
| (:Node {id: 2})  | 0.5              |
| (:Node {id: 8})  | 0.1              |
| (:Node {id: 3})  | 0                |
| (:Node {id: 4})  | 0                |
| (:Node {id: 5})  | 0                |
| (:Node {id: 6})  | 0                |
| (:Node {id: 7})  | 0                |
| (:Node {id: 9})  | 0.1              |
+------------------+------------------+