katz_centrality_online (Enterprise)
From Memgraph 3.0, dynamic graph algorithms became a part of the Memgraph Enterprise license. To use dynamic graph algorithms, you need to enable Memgraph Enterprise license. If you want to know more and learn how this affects you, read our announcement.
Because of its simplicity, Katz Centrality has become one of the most established centrality measurements. The definition of Katz centrality is that it presents the amount of influence by summing all walks starting from the node of interest and weighting walks by some attenuation factor smaller than 1.
Just as the other centrality measures got their dynamic algorithm implementations, so did Katz Centrality. The implementation results in a reduction of computations needed to update already calculated results. The algorithm offers substantially large speedups compared to static algorithm runs.
The algorithm is based on the work of Alexander van der Grinten et. al. called Scalable Katz Ranking Computation in Large Static and Dynamic Graphs. The author proposes an estimation method that computes Katz’s centrality by iteratively improving upper and lower bounds on the centrality scores. The computed scores may differ from the real values, but the algorithm has the guarantee of preserving the rankings.
Online Katz centrality should be used in a specific way. To set the parameters,
use the set() procedure, which will also set the context of the streaming
algorithm. The get() procedure returns the resulting values stored in a cache.
Therefore, if you try to get values before first calling set(), the run will
fail with a proper message.
To make the incremental flow, you should set the proper trigger using the
update() function:
CREATE TRIGGER katz_trigger
(BEFORE | AFTER) COMMIT
EXECUTE CALL katz_centrality_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;Finally, the reset() function resets the context and enables new runs.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | directed |
| Edge weights | unweighted |
| Parallelism | sequential |
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
set()
Use the procedure to calculate Katz Centrality.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
alpha: double (default=0.2)➡ Exponential decay factor defining the walk length importance. -
epsilon: double (default=1e-2)➡ Convergence tolerance. Minimal difference in two adjacent pairs of nodes in the final ranking.
Output:
node➡ Node in the graph, for which Katz Centrality is calculated.rank➡ Normalized ranking of a node. Expresses the centrality value after bound convergence.
Usage:
To calculate Katz Centrality, use the following query:
CALL katz_centrality_online.set(0.2, 0.01)
YIELD node, rank;get()
The get() procedure should be used once the trigger has been set or the set()
procedure has been called before adding changes to the graph.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
Output:
node➡ Node in the graph, for which Katz Centrality is calculated.rank➡ Normalized ranking of a node. Expresses the centrality value after bound convergence.
Usage:
To get the Katz Centrality values, use the following query:
CALL katz_centrality_online.get()
YIELD node, rank;update()
The procedure is used to update the Katz Centrality values.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
created_vertices➡ Vertices (nodes) that were created in the last transaction. -
created_edges➡ Edges (relationships) created in a period from the last transaction. -
deleted_vertices➡ Vertices (nodes) deleted from the last transaction. -
deleted_edges➡ Edges (relationships) deleted from the last transaction.
Output:
node➡ Node in the graph, for which Katz Centrality is calculated.rank➡ Normalized ranking of a node. Expresses the centrality value after bound convergence.
Usage:
The procedure is used with triggers in order to update the values upon changes to the graph:
CREATE TRIGGER katz_trigger
(BEFORE | AFTER) COMMIT
EXECUTE CALL katz_centrality_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;Example
Create a trigger
The following query sets a trigger which will update the values upon creating new data or deleting existing data:
CALL katz_centrality_online.set(0.2)
YIELD node, rank
RETURN node, rank;
CREATE TRIGGER katz_trigger
BEFORE COMMIT
EXECUTE CALL katz_centrality_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;Add new data
New data is added to the database:
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);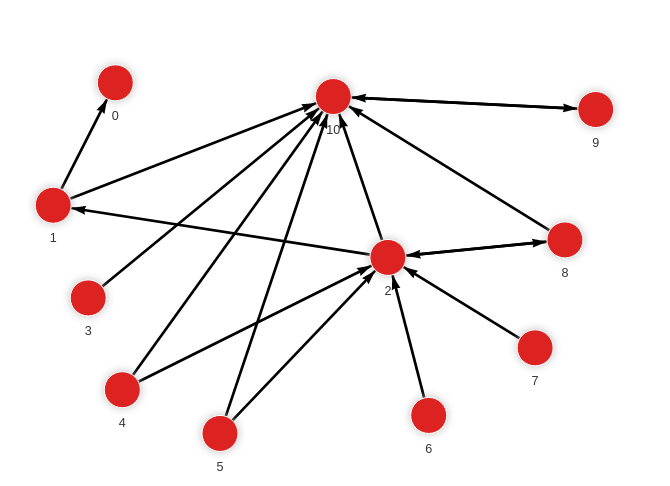
As new data is added, the triggered katz_centrality_online.update() procedure calculates the values.
Get Katz centrality
Return the values using the following query:
MATCH (node)
RETURN node.id AS node_id, node.rank AS rank;Results:
+---------+---------+
| node_id | rank |
+---------+---------+
| 1 | 0.408 |
| 0 | 0.28 |
| 10 | 1.864 |
| 2 | 1.08 |
| 8 | 0.408 |
| 3 | 0 |
| 4 | 0 |
| 5 | 0 |
| 6 | 0 |
| 7 | 0 |
| 9 | 0.544 |
+---------+---------+