set_cover
The Set Cover problem is one of the problems in graph theory that tries to solve the least possible set of sets that covers all elements inside those sets. Given a set of n elements, and a collection of m sets containing them, the algorithm tries to identify the smallest sub-collection of sets whose union equal to all the elements. It is NP-complete, however solvable with techniques such as constraint programming. The current algorithm uses GEKKO optimizer as a constraint programming solver.
| Trait | Value |
|---|---|
| Module type | module |
| Implementation | Python |
| Graph direction | undirected |
| Edge weights | unweighted |
| Parallelism | sequential |
Too slow?
If this algorithm implementation is too slow for your use case, open an issue on Memgraph’s GitHub repository and request a rewrite to C++!
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
cp_solve()
Input:
The input itself represents an element-set pair with each row of the lists.
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
element_vertexes: List[Vertex]➡ List of element nodes in pairs. -
set_vertexes: List[Vertex]➡ List of set nodes in pairs.
Output:
containing_set➡ The minimal set of sets in which all the elements are contained.
Usage:
To get the minimal set of sets, run the following query:
CALL set_cover.cp_solve([(:Point), (:Point)], [(:Set), (:Set)])
YIELD containing_set;greedy()
The greedy algorithm quickly selects local optima without guaranteeing a global optimum. So, not bad, not terrible.
Input:
The input itself represents an element-set pair with each row of the lists.
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
element_vertexes: List[Vertex]➡ List of element nodes in pairs. -
set_vertexes: List[Vertex]➡ List of set nodes in pairs.
Output:
containing_set➡ The minimal set of sets in which all the elements are contained.
Usage:
To get the minimal set of sets using the greedy algorithm, run the following query:
CALL set_cover.greedy([(:Point), (:Point)], [(:Set), (:Set)])
YIELD containing_set;Example
Database state
The database contains the following data:
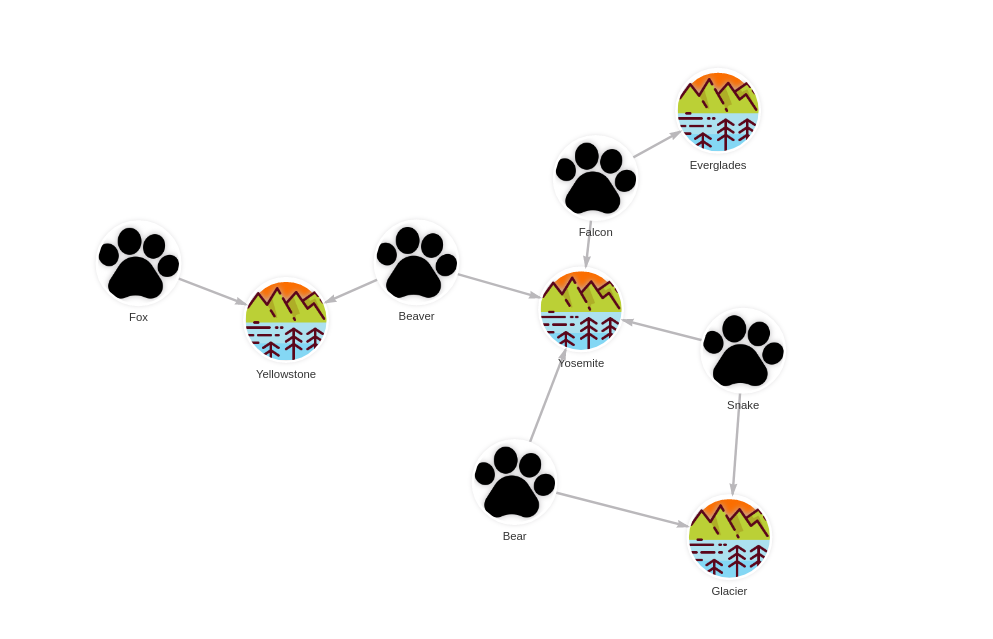
Created with the following Cypher queries:
CREATE (e:AnimalSpecies {name: 'Snake'});
CREATE (e:AnimalSpecies {name: 'Bear'});
CREATE (e:AnimalSpecies {name: 'Falcon'});
CREATE (e:AnimalSpecies {name: 'Beaver'});
CREATE (e:AnimalSpecies {name: 'Fox'});
CREATE (s:NationalPark {name: 'Yosemite'});
CREATE (s:NationalPark {name: 'Grand Canyon'});
CREATE (s:NationalPark {name: 'Yellowstone'});
CREATE (s:NationalPark {name: 'Glacier'});
CREATE (s:NationalPark {name: 'Everglades'});
MATCH (e: AnimalSpecies {name: 'Snake'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Bear'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Falcon'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Beaver'}), (s:NationalPark {name: 'Yosemite'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Fox'}), (s:NationalPark {name: 'Yellowstone'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Beaver'}), (s:NationalPark {name: 'Yellowstone'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Snake'}), (s:NationalPark {name: 'Glacier'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Bear'}), (s:NationalPark {name: 'Glacier'})
CREATE (e)-[:LIVES_IN]->(s);
MATCH (e: AnimalSpecies {name: 'Falcon'}), (s:NationalPark {name: 'Everglades'})
CREATE (e)-[:LIVES_IN]->(s);Get minimal set of sets
To get the minimal set of sets, run the following query:
MATCH (e:AnimalSpecies)-[l:LIVES_IN]-(s:NationalPark)
WITH collect(e) AS animal_list, collect(s) AS park_list
CALL set_cover.cp_solve(animal_list, park_list)
YIELD containing_set
WITH containing_set AS national_park
MATCH (animal:AnimalSpecies)-[l:LIVES_IN]->(national_park)
RETURN animal, l, national_park;Result: