graph_coloring
Graph coloring is the assignment of colors to nodes such that two nodes connected with a relationship don’t have the same color. The goal is to minimize the number of colors while correctly coloring a graph.
Algorithm implementation is inspired by “Quantum Annealing (QA)”, a simple metaheuristic frequently used for solving discrete optimization problems.
QA is a simple strategy for exploring a solution space. The main idea is to start a search with several possible solutions. These solutions change through iterations and produce new “better” solutions. Each solution has a particular error value which depends on the error function that the algorithm optimizes. In the graph coloring scenario, the error function is often defined as the number of edges connecting nodes with the same color.
The algorithm is iterative. It applies several simple rules to change solutions in a loop (the same rules are applied multiple times). The algorithm terminates when a stop criterion is met, usually when the error becomes zero. One of the rules could be to randomly select the node involved in a conflict and change its colors.
Changes made in one iteration may not be permanent if they don’t improve the solution. But, with a certain probability, the new solution is accepted even if its error is not reduced. In that way, the algorithm is prevented from converging to local minimums too early.
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | Python |
| Graph direction | undirected |
| Edge weights | weighted/unweighted |
| Parallelism | parallel |
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
color_graph()
The procedure assigns colors to nodes in the whole graph such that two nodes connected with a relationship don’t have the same color.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
parameters: Dict[string, Any] (default={})➡ A dictionary that specifies the algorithm configuration by listing parameters. -
edge_property: string (default=weight)➡ Relationship property that stores the relationship weight. Any relationship attribute not present defaults to 1.
Output:
node: Vertex➡ Represents the node.color: int➡ Represents the assigned color.
Usage:
Use the following query assign colors:
CALL graph_coloring.color_graph()
YIELD node, color; color_subgraph()
The procedure assigns colors to nodes in a subgraph such that two nodes connected with a relationship don’t have the same color.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
vertices: List[Vertex]➡ List of vertices in the subgraph. -
edges: List[Edge]➡ List of relationships in the subgraph. -
parameters: Dict[string, Any] (default={})➡ A dictionary that specifies the algorithm configuration by listing parameters. -
edge_property: string (default=weight)➡ Relationship property that stores the relationship weight. Any relationship attribute not present defaults to 1.
Output:
node: Vertex➡ Represents the node.color: int➡ Represents the assigned color.
Usage:
Use the following query to assign colors on a subgraph:
MATCH (a)-[e]->(b)
WITH collect(a) as nodes, collect (e) as edges
CALL graph_coloring.color_subgraph(nodes, edges, {no_of_colors: 2})
YIELD node, color;Parameters
| Name | Type | Default | Description |
|---|---|---|---|
| algorithm | String | QA | An optimization strategy used to find graph coloring. |
| no_of_colors | Integer | 10 | The number of colors used to color the nodes of the graph. |
| no_of_processes | Integer | 1 | The number of processes used to execute the algorithm in parallel. |
| population_size | Integer | 15 | The number of different solutions that are improved through iterations. |
| population_factory | String | ChainChunkFactory | The name of a function that generates an initial population. |
| init_algorithms | List[String] | [SDO, LDO] | Contains algorithms used to initialize the solutions. |
| error | String | ConflictError | The name of an error function that is minimized by an optimization strategy. |
| max_iterations | Integer | 10 | The maximum number of iterations of an algorithm. |
| iteration_callbacks | List[String] | [] | Contains iteration callbacks. Iteration callback is called after each iteration of the iterative algorithm. Iteration callback saves certain population information and calls specified actions if certain conditions are met. |
| communication_delay | Integer | 10 | The number of iterations that must pass for neighboring parts to exchange solutions. |
| logging_delay | Integer | 10 | The number of iteration after the algorithm information is logged. |
| QA_temperature | Float | 0.035 | The temperature parameter of the quantum annealing algorithm. |
| QA_max_steps | Float | 10 | The maximum number of steps in one iteration. |
| conflict_err_alpha | Float | 0.1 | The number that scales the sum of the conflicting edges in the error function formula. |
| conflict_err_beta | Float | 0.001 | The number that scales the correlation between solutions in the error function formula. |
| mutation | String | SimpleMutation | The name of a function that changes the solutions. |
| multiple_mutation_no_of_nodes | Integer | 2 | The number of nodes that will change color. |
| random_mutation_probability | Float | 0.1 | The probability that the color of the random node (it does not have to be conflicting) will be changed. |
| simple_tunneling_mutation | String | MultipleMutation | The name of a mutation function. |
| simple_tunneling_probability | Float | 0.5 | The probability of changing an individual. |
| simple_tunneling_error_correction | Float | 2 | The mutated individual is accepted only if its error is less than the error of the old individual multiplied by this parameter. |
| simple_tunneling_max_attempts | Integer | 25 | The maximum number of mutation attempts until the individual is accepted. |
| convergence_callback_tolerance | Integer | 500 | The maximum number of iterations in which if the algorithm does not find a better solution convergence occurs and defined actions are called. |
| convergence_callback_actions | String | [SimpleTunneling] | Actions that are called when convergence is detected. |
Example
Database state
The database contains the following data:
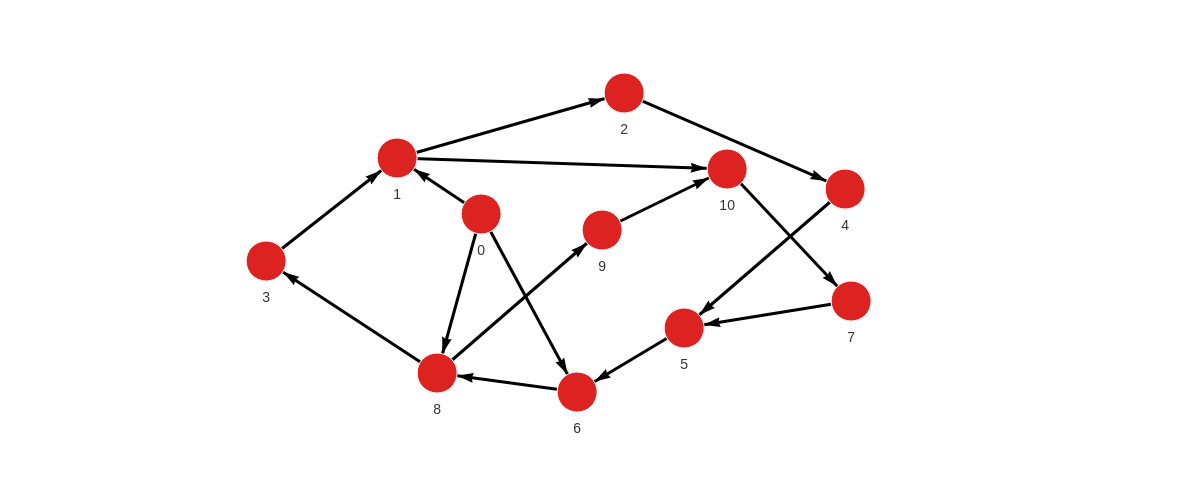
Created with the following Cypher queries:
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 7}) CREATE (a)-[:RELATION]->(b);Apply graph coloring
Get the values using the following query:
CALL graph_coloring.color_graph({no_of_colors: 4})
YIELD node, color
RETURN node, color;Results:
+-------+-------+
| node | color |
+-------+-------+
| "130" | "1" |
| "131" | "3" |
| "132" | "0" |
| "133" | "1" |
| "134" | "2" |
| "135" | "1" |
| "136" | "3" |
| "137" | "0" |
| "138" | "0" |
| "139" | "3" |
| "140" | "1" |
+-------+-------+