Advanced algorithms
Available algorithms
betweenness_centrality

betweenness_centrality

In network studies, centrality analysis illuminates the significance of nodes, with betweenness centrality being one of the most important metrics. It determines the importance of a node based on how frequently it lies on the shortest paths between other nodes, signifying its influence on information flow within the network. Such nodes, possessing high betweenness, often act as gatekeepers in controlling the transmission of information.

While the concept of betweenness centrality revolves around shortest paths, defined by the fewest relationships or minimal cumulative relationship weight in weighted graphs, the calculation methodologies can vary. One notable method is described in the paper "A Faster Algorithm for Betweenness Centrality" (opens in a new tab)(Brandes, 2001).

Source code
TraitValue
Module typealgorithm
ImplementationC++
Graph directiondirected/undirected
Edge weightsunweighted
Parallelismparallel

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

get()

The procedure returns the betweenness centrality values.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • directed: boolean (default=True) ➡ If False the direction of the relationships is ignored.

  • normalized: boolean (default=True) ➡ If True the betweenness values are normalized by 2/((n-1)(n-2)) for graphs, and 1/((n-1)(n-2)) for directed graphs where n is the number of nodes.

  • threads: integer (default=number of concurrent threads supported by the implementation) ➡ The number of threads used to calculate betweenness centrality.

Output:

  • betweenness_centrality: float ➡ The value of betweenness centrality for a given node.
  • node: Vertex ➡ Graph node for betweenness calculation.

Usage: 

CALL betweenness_centrality.get()
YIELD node, betweenness_centrality;

Example

Database state

The database contains the following data:

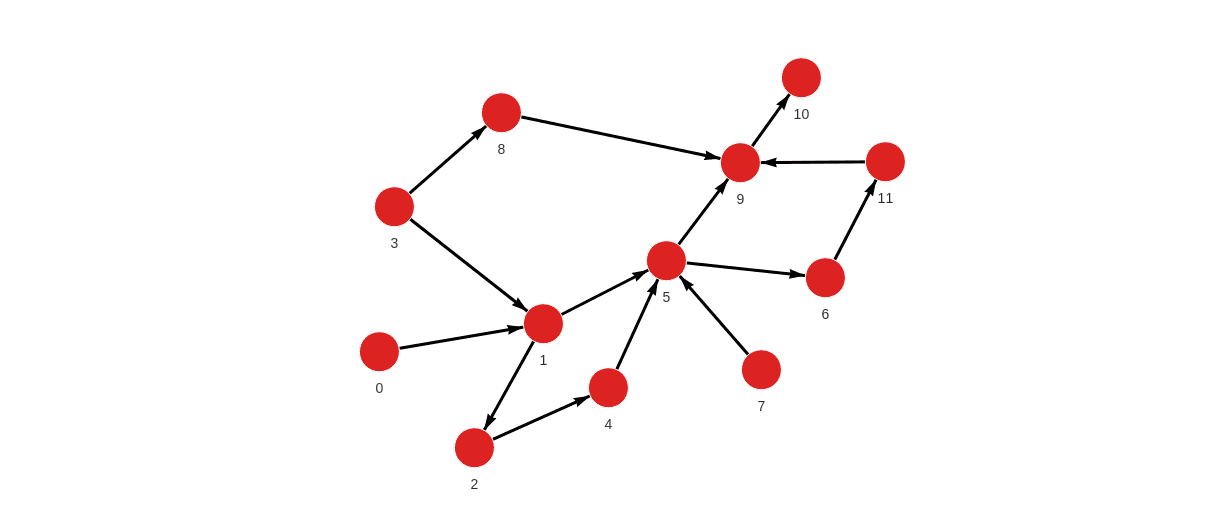
Created with the following Cypher queries:

MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 11}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 11}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);

Calculate betwenness centrality

Get the values using the following query:

CALL betweenness_centrality.get(TRUE,TRUE)
YIELD node, betweenness_centrality
RETURN node, betweenness_centrality;

Results:

+-------------------------+-------------------------+
| node                    | betweenness_centrality  |
+-------------------------+-------------------------+
| (:Node {id: 0})         | 0                       |
| (:Node {id: 1})         | 0.109091                |
| (:Node {id: 2})         | 0.0272727               |
| (:Node {id: 3})         | 0                       |
| (:Node {id: 4})         | 0.0454545               |
| (:Node {id: 5})         | 0.2                     |
| (:Node {id: 6})         | 0.0636364               |
| (:Node {id: 7})         | 0                       |
| (:Node {id: 8})         | 0.0181818               |
| (:Node {id: 9})         | 0.0909091               |
| (:Node {id: 10})        | 0                       |
| (:Node {id: 11})        | 0.0181818               |
+-------------------------+-------------------------+