Advanced algorithms
Available algorithms
node_similarity

node_similarity

If you want to find out how similar two nodes in a graph are, you need to get a numerical value that represents the node similarity between those two nodes. There are many node similarity measures and currently this module contains the following:

  • Jaccard similarity
  • overlap similarity
  • cosine similarity

The Jaccard similarity is computed using the following formula:

Jaccard(A,B)=∣A∩B∣∣A∣+∣B∣−∣A∩B∣Jaccard(\mathcal{A}, \mathcal{B}) = \frac{|\mathcal{A} \cap \mathcal{B}|}{|\mathcal{A}| + |\mathcal{B}| - |\mathcal{A} \cap \mathcal{B}|}

The overlap similarity is computed using the following formula:

Overlap(A,B)=∣A∩B∣min⁡(∣A∣,∣B∣)Overlap(\mathcal{A}, \mathcal{B}) = \frac{|\mathcal{A} \cap \mathcal{B}|}{\min(|\mathcal{A}|, |\mathcal{B}|)}

The cosine similarity computes similarity between two nodes based on some property. This property should be a vector and it can be computed using the following formula:

Cosine(A,B,property)=∑i=1nA[propertyi]×B[propertyi]∑i=1nA[propertyi]2×∑i=1nB[propertyi]2\text{Cosine}(A, B, \text{property}) = \frac{\sum_{i=1}^{n} A[\text{property}_i] \times B[\text{property}_i]}{\sqrt{\sum_{i=1}^{n} A[\text{property}_i]^2} \times \sqrt{\sum_{i=1}^{n} B[\text{property}_i]^2}}

Set A represents all outgoing neighbors of one node, set B represents all outgoing neighbors of the other node. In all the given formulas, the numerator is the cardinality of the intersection of set A and set B (in other words, the cardinality of the common neighbors set). The denominator differs but requires the cardinality of sets A and B in some way.

For each similarity measure, there are two functions, one that calculates similarity between all pairs of nodes and the other, pairwise function, that takes into account pairwise similarities between two set of nodes.

Source code
TraitValue
Module typealgorithm
ImplementationC++
Graph directiondirected
Edge weightsunweighted
Parallelismsequential

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

jaccard()

The following procedure will calculate the Jaccard similarity between all pairs of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The Jaccard similarity between the first and the second node.

Usage:

To calculate Jaccard similarity, use the following query:

CALL node_similarity.jaccard() YIELD node1, node2, similarity
RETURN node1, node2, similarity;

jaccard_pairwise()

The following procedure will calculate the Jaccard similarity taking into account pairwise similarities between two set of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • src_nodes: List[Vertex] ➡ The first set of nodes.

  • dst_nodes: List[Vertex] ➡ The second set of nodes.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The Jaccard similarity between the first and the second node.

Usage:

To calculate Jaccard similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.jaccard_pairwise(nodes1, nodes2) YIELD node1, node2, similarity AS jaccard_similarity
RETURN node1, node2, jaccard_similarity;

overlap()

The following procedure will calculate the overlap similarity between all pairs of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The overlap similarity between the first and the second node.

Usage:

To calculate overlap similarity, use the following query:

CALL node_similarity.overlap() YIELD node1, node2, similarity
RETURN node1, node2, similarity;

overlap_pairwise()

The following procedure will calculate the overlap similarity taking into account pairwise similarities between two set of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • src_nodes: List[Vertex] ➡ The first set of nodes.

  • dst_nodes: List[Vertex] ➡ The second set of nodes.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The overlap similarity between the first and the second node.

Usage:

To calculate Jaccard similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.overlap_pairwise(nodes1, nodes2) YIELD node1, node2, similarity AS overlap_similarity
RETURN node1, node2, overlap_similarity;

cosine()

The following procedure will calculate the cosine similarity between all pairs of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • node1: Vertex ➡ The first node.

  • node2: Vertex ➡ The second node.

  • property: str ➡ The property based on which the cosine similarity will be calculated. If the property is not of the vector type, the error will be thrown.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The cosine similarity between the first and the second node.

Usage:

To calculate cosine similarity, use the following query:

CALL node_similarity.cosine("score") YIELD node1, node2, similarity
RETURN node1, node2, similarity

cosine_pairwise()

The procedure calculates the cosine similarity taking into account pairwise similarities between two set of nodes.

Input:

  • subgraph: Graph (OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by the project() function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.

  • src_nodes: List[Vertex] ➡ The first set of nodes.

  • dst_nodes: List[Vertex] ➡ The second set of nodes.

  • property: str ➡ The property based on which the cosine similarity will be calculated. If the property is not of the vector type, the error will be thrown.

Output:

  • node1: Vertex ➡ The first node.
  • node2: Vertex ➡ The second node.
  • similarity: float ➡ The cosine similarity between the first and the second node.

Usage:

To calculate cosine similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.cosine_pairwise("score", nodes1, nodes2) YIELD node1, node2, similarity
RETURN node1, node2, similarity

Example

Database state

The database contains the following data:

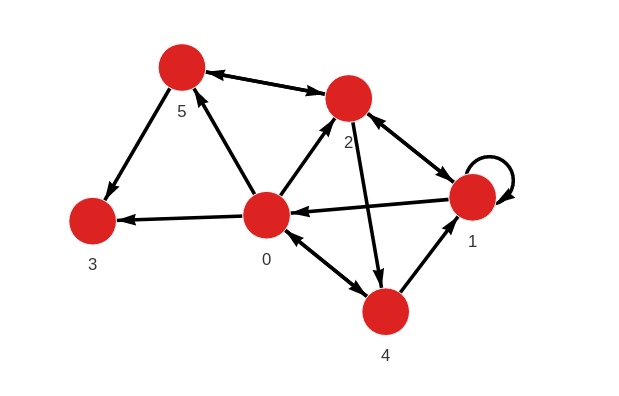
Created with the following Cypher queries:

CREATE (b:Node {id: 0, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 1, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 2, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 3, score: [1.0, 1.0, 0.0]});
CREATE (b:Node {id: 4, score: [0.0, 1.0, 0.0]});
CREATE (b:Node {id: 5, score: [1.0, 0.0, 1.0]});
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);

Jaccard pairwise similarity

To calculate Jaccard similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.jaccard_pairwise(nodes1, nodes2) YIELD node1, node2, similarity AS jaccard_similarity
RETURN node1, node2, jaccard_similarity;

Results:

+-------------------+-------------------+--------------------+
| node1             | node2             | jaccard_similarity |
+-------------------+-------------------+--------------------+
| (:Node {id: 1})   | (:Node {id: 3})   | 0.0                |
| (:Node {id: 2})   | (:Node {id: 4})   | 0.25               |
| (:Node {id: 0})   | (:Node {id: 5})   | 0.5                |
+-------------------+-------------------+--------------------+

Overlap pairwise similarity

To calculate overlap similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.overlap_pairwise(nodes1, nodes2) YIELD node1, node2, similarity AS overlap_similarity
RETURN node1, node2, overlap_similarity;

Results:

+-------------------+-------------------+--------------------+
| node1             | node2             | overlap_similarity |
+-------------------+-------------------+--------------------+
| (:Node {id: 1})   | (:Node {id: 3})   | 0.0                |
| (:Node {id: 2})   | (:Node {id: 4})   | 0.5                |
| (:Node {id: 0})   | (:Node {id: 5})   | 1.0                |
+-------------------+-------------------+--------------------+

Cosine pairwise similarity

To calculate cosine similarity taking into account pairwise similarities, use the following query:

MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.cosine_pairwise("score", nodes1, nodes2) YIELD node1, node2, similarity AS cosine_similarity
RETURN node1, node2, cosine_similarity;

Results:

+-------------------+-------------------+-------------------+
| node1             | node2             | cosine_similarity |
+-------------------+-------------------+-------------------+
| (:Node {id: 1})   | (:Node {id: 3})   | 0.816             |
| (:Node {id: 2})   | (:Node {id: 4})   | 0.577             |
| (:Node {id: 0})   | (:Node {id: 5})   | 0.816             |
+-------------------+-------------------+-------------------+