max_flow
The maximum flow problem consists of finding a flow through a graph such that it is the maximum possible flow.
The algorithm implementation is based on the Ford-Fulkerson method with capacity scaling. Ford-Fulkerson method is not itself an algorithm as it does not specify the procedure of finding augmenting paths in a residual graph. It is a greedy method, using augmenting paths as it comes across them. Input is a weighted graph with a defined source and sink, representing the beginning and end of the flow network. The algorithm begins with an empty flow and, at each step, finds a path, called an augmenting path, from the source to the sink that generates more flow. When flow cannot be increased anymore, the algorithm stops, and the maximum flow has been found.
The capacity scaling is a heuristic for finding augmenting paths in such a way that prioritizes taking edges with larger capacities, maintaining a threshold value that is only lowered once no larger path can be found. It speeds up the algorithm noticeably compared to a standard DFS search.
The algorithm is adapted to work with heterogeneous graphs, meaning not all edges need to have the defined edge property used for edge flow. When an edge doesn’t have a flow, it is skipped, and when no edges have this property, the returning max flow value is 0.
| Trait | |
|---|---|
| Module type | algorithm |
| Implementation | Python |
| Graph direction | directed |
| Edge weights | weighted |
| Parallelism | sequential |
Too slow?
If this algorithm implementation is too slow for your use case, open an issue on Memgraph’s GitHub repository and request a rewrite to C++!
Procedures
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
get_flow()
Use the get_flow() procedure to calculate the maximum flow.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
start_v: Vertex➡ Source node from which the maximum flow is calculated. -
end_v: Vertex➡ Sink node to which the max flow is calculated. -
edge_property: string (default="weight")➡ Relationship property which is used as the flow capacity of the relationship.
Output:
max_flow: Number➡ Maximum flow of the network, from the source node to the sink node.
Usage:
To calculate the maximum flow, use the following query:
MATCH (source {id: 0}), (sink {id: 5})
CALL max_flow.get_flow(source, sink, "weight")
YIELD max_flow
RETURN max_flow;get_paths()
The get_paths() procedure returns paths that are a part of the flow with the maximum flow.
Input:
-
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default. -
start_v: Vertex➡ Source node from which the maximum flow is calculated. -
end_v: Vertex➡ Sink node to which the max flow is calculated. -
edge_property: string (default="weight")➡ Relationship property which is used as the flow capacity of the relationship.
Output:
path: Path➡ The path with a flow in a maximum flow.flow: Number➡ The flow amount corresponding to that path.
Usage:
To get the paths creating the maximum flow, use the following query:
MATCH (source {id: 0}), (sink {id: 5})
CALL max_flow.get_paths(source, sink, "weight")
YIELD path, flow
RETURN path, flow;Example
Database state
The database contains the following data:
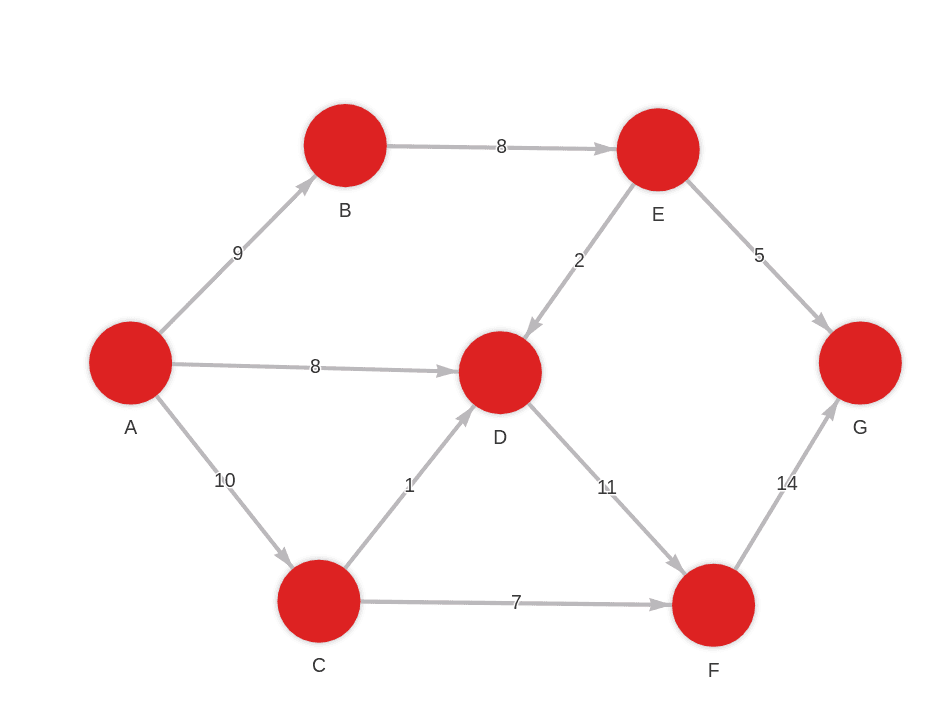
Created with the following Cypher queries:
MERGE (a:Node {id: "A"}) MERGE (b:Node {id: "B"}) CREATE (a)-[:RELATION {weight: 9}]->(b);
MERGE (a:Node {id: "A"}) MERGE (b:Node {id: "C"}) CREATE (a)-[:RELATION {weight: 10}]->(b);
MERGE (a:Node {id: "B"}) MERGE (b:Node {id: "E"}) CREATE (a)-[:RELATION {weight: 8}]->(b);
MERGE (a:Node {id: "C"}) MERGE (b:Node {id: "F"}) CREATE (a)-[:RELATION {weight: 7}]->(b);
MERGE (a:Node {id: "C"}) MERGE (b:Node {id: "D"}) CREATE (a)-[:RELATION {weight: 1}]->(b);
MERGE (a:Node {id: "A"}) MERGE (b:Node {id: "D"}) CREATE (a)-[:RELATION {weight: 8}]->(b);
MERGE (a:Node {id: "E"}) MERGE (b:Node {id: "D"}) CREATE (a)-[:RELATION {weight: 2}]->(b);
MERGE (a:Node {id: "D"}) MERGE (b:Node {id: "F"}) CREATE (a)-[:RELATION {weight: 11}]->(b);
MERGE (a:Node {id: "E"}) MERGE (b:Node {id: "G"}) CREATE (a)-[:RELATION {weight: 5}]->(b);
MERGE (a:Node {id: "F"}) MERGE (b:Node {id: "G"}) CREATE (a)-[:RELATION {weight: 14}]->(b);Calculate maximum flow
Calculate the maximum flow using the following query:
MATCH (source {id: "A"}), (sink {id: "G"})
CALL max_flow.get_flow(source, sink)
YIELD max_flow
RETURN max_flow;Results:
+----------+
| max_flow |
+----------+
| 19 |
+----------+