Advanced algorithms
Available algorithms
katz_centrality

katz_centrality

Katz Centrality is the measurement of centrality that incorporates the inbound path length starting from the wanted node. More central nodes will have closer connections rather than having many long-distance nodes connected to them.

The implemented algorithm is based on the work of Alexander van der Grinten et. al. called Scalable Katz Ranking Computation in Large Static and Dynamic Graphs (opens in a new tab). The author proposes an estimation method that preserves rankings for both static and dynamic Katz centrality scenarios.

Theoretically speaking there exists an attenuation factor (alpha^i) smaller than 1 which is applied to walks of length i. If w_i(v) is the number of walks of length i starting from node v, Katz centrality is defined as:

Centrality(v) = sum { w_i(v) * alpha ^ i}

The constructed algorithm computes Katz centrality by iteratively improving the upper and lower bounds on centrality scores. This guarantees that centrality rankings will be correct, but it does not guarantee that the corresponding resulting centralities will be correct.

Source code
TraitValue
Module typealgorithm
ImplementationC++
Graph directiondirected
Edge weightsunweighted
Parallelismsequential

Procedures

You can execute this algorithm on graph projections, subgraphs or portions of the graph.

get()

The procedure calculates Katz Centrality.

Input:

  • alpha: double (default=0.2) ➡ Exponential decay factor defining the walk length importance.
  • epsilon: double (default=1e-2) ➡ Convergence tolerance. Minimal difference in two adjacent pairs of nodes in the final ranking.

Output:

  • node ➡ Node in the graph, for which Katz Centrality is calculated.
  • rank ➡ Normalized ranking of a node. Expresses the centrality value after bound convergence

Usage:

Use the following query to calculate Katz Centrality:

CALL katz_centrality.get()
YIELD node, rank;

Example

Database state

The database contains the following data:

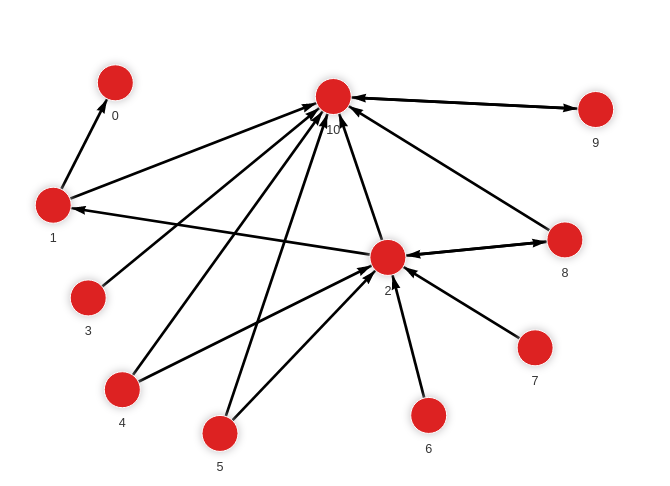
Created with the following Cypher queries:

MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 8}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 6}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 7}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 8}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 9}) MERGE (b:Node {id: 10}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 10}) MERGE (b:Node {id: 9}) CREATE (a)-[:RELATION]->(b);

Calculate Katz centrality

Get values using the following query:

CALL katz_centrality.get()
YIELD node, rank
RETURN node, rank;

Results:

+------------------+------------------+
| node             | rank             |
+------------------+------------------+
| (:Node {id: 9})  | 0.544            |
| (:Node {id: 7})  | 0                |
| (:Node {id: 6})  | 0                |
| (:Node {id: 5})  | 0                |
| (:Node {id: 4})  | 0                |
| (:Node {id: 3})  | 0                |
| (:Node {id: 8})  | 0.408            |
| (:Node {id: 2})  | 1.08             |
| (:Node {id: 10}) | 1.864            |
| (:Node {id: 0})  | 0.28             |
| (:Node {id: 1})  | 0.408            |
+------------------+------------------+