Deep path traversal algorithms

Graph algorithms are a set of instructions that traverse (visits nodes of) a graph and find specific nodes, paths, or a path between two nodes. Some of these algorithms are built into Memgraph and don't require any additional libraries:

• Depth-first search (DFS)
• Breadth-first search (BFS)
• Weighted shortest path (WSP)
• All shortest paths (ASP)

Below you can find examples of how to use these algorithms and you can try them out in the Playground sandbox (opens in a new tab) using the Europe backpacking dataset or adjust them to the dataset of your choice.

Depth-first search

Depth-first search (DFS) is an algorithm for traversing through the graph. The algorithm starts at the root node and explores each neighboring node as far as possible. The moment it reaches a dead-end, it backtracks until it finds a new, undiscovered node, then traverses from that node to find more undiscovered nodes. In that way, the algorithm visits each node in the graph.

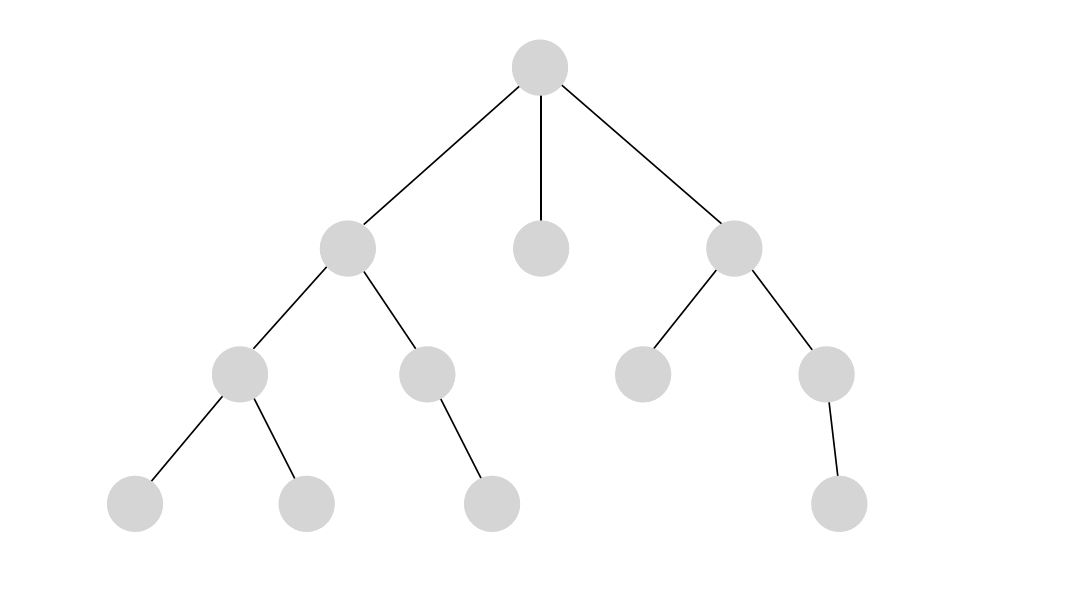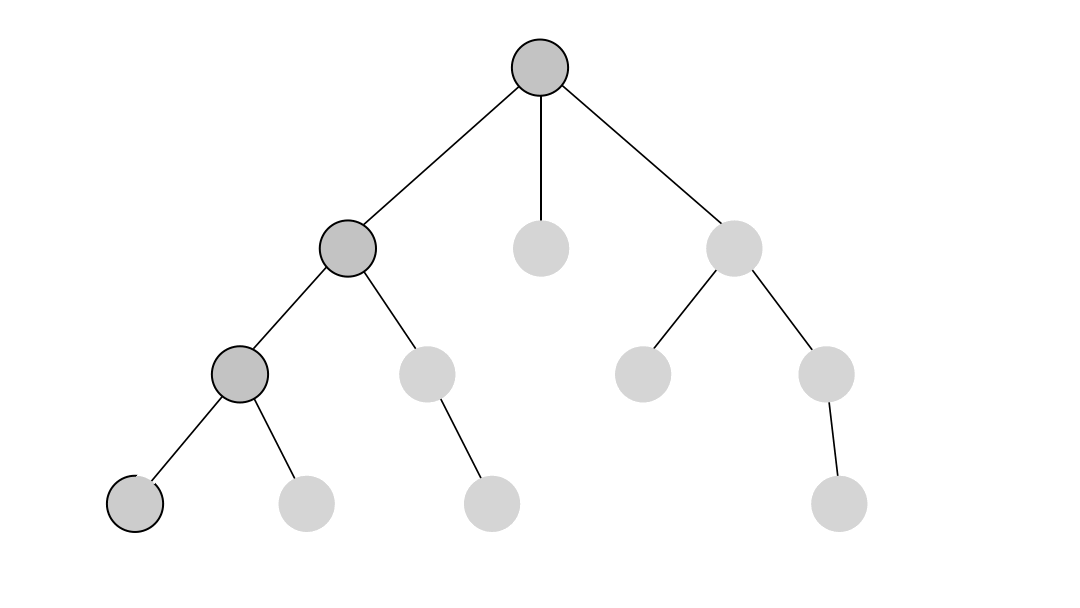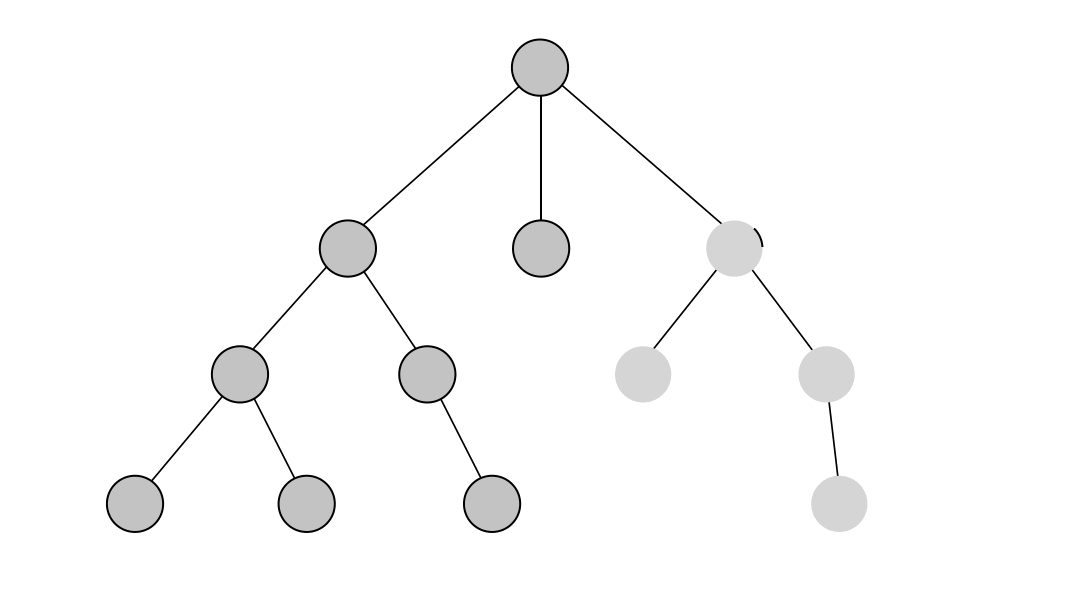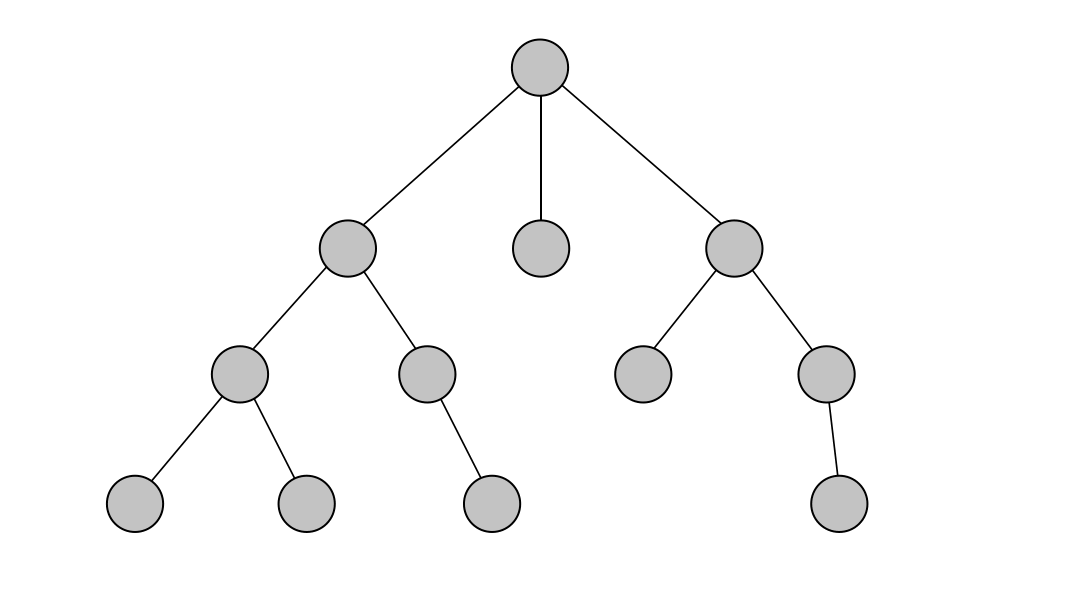
DFS in Memgraph has been implemented based on the relationship expansion syntax which allows it to find multiple relationships between two nodes if such exist and returns all paths between the given nodes.

Below is an example of running the DFS on a simple dataset. The output of the algorithm are all of the paths between the given start and end node found with the depth-first search traversal.

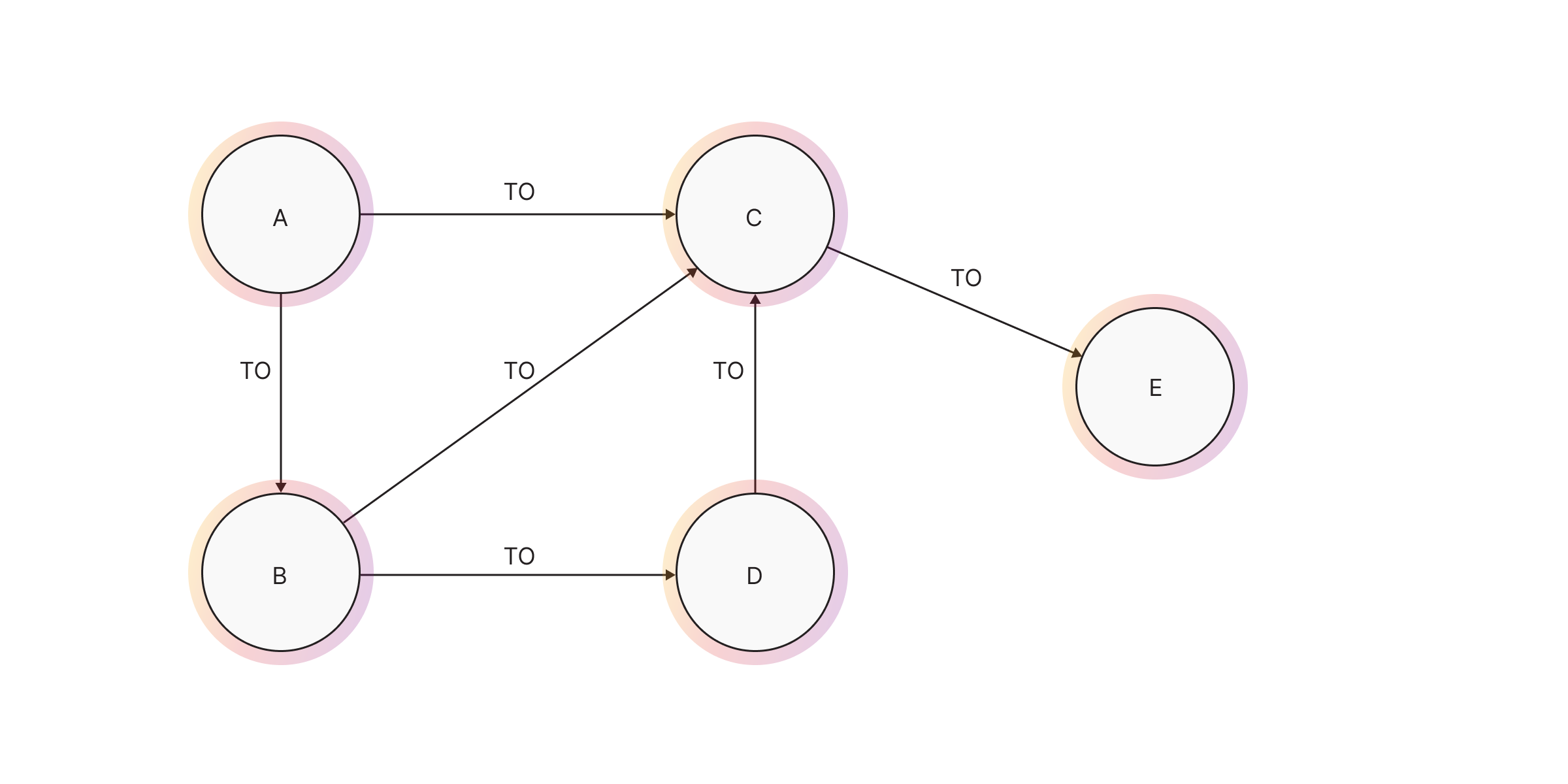
When to use DFS?

DFS returns all found paths between given nodes and is the most suitable for determining path existence between two nodes in a graph. If the output of the algorithm is null, there are no available paths between the nodes. If the output is not null, the DFS algorithm is going to provide all possible paths as a result.

Getting various results

The following query will show all the paths from node n to node m:

MATCH path=(n {id: 0})-[*]->(m {id: 8})
RETURN path;

To get the list of all relationships, add a variable in the square brackets and return it as a result:

MATCH (n {id: 0})-[relationships *]->(m {id: 8})
RETURN relationships;

To get the list of path nodes, use the nodes() function:

MATCH path=(n {id: 0})-[*]->(m {id: 8})
RETURN path,nodes(path);

Filtering by relationships type and direction

You can filter relationships by type by defining the type after the relationship list variable, and you decide the direction by adding or removing an arrow from the dash.

In the following example, the algorithm will traverse only across CloseTo type of relationships:

MATCH path=(n {id: 0})-[relationships:CloseTo *]->(m {id: 8})
RETURN path,relationships;

You can also list multiple relationship types and allow your algorithm to traverse across any of them.

In the following example, the algorithm will traverse across any of the CloseTo, Borders or the Inside type of relationship:

MATCH path=(n {id: 0})-[relationships:CloseTo | :Borders | :Inside *]->(m {id: 8})
RETURN path,relationships;

Be careful when using algorithms, especially DFS, without defining a direction. Depending on the size of the dataset, the execution of the query can cause a timeout.

Constraining the path's length

The constraints on the path length are defined after the asterisk sign. The following query will return all the results when the path is equal to or shorter than 5 hops:

MATCH path=(n {id: 0})-[relationships * ..5]->(m {id: 8})
RETURN path,relationships;

This query will return all the paths that are equal to or longer than 3, and equal to or shorter than 5 hops:

MATCH path=(n {id: 0})-[relationships * 3..5]->(m {id: 8})
RETURN path,relationships;

Constraining the expansion based on property values

Depth-first expansion allows an arbitrary expression filter that determines if an expansion is allowed over a certain relationship to a certain node. The filter is defined as a lambda function over r and n, which denotes the relationship expanded over and node expanded to in the depth-first search.

In the following example, expansion is allowed over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15:

MATCH path=(n {id: 0})-[* (r, n | r.eu_border = false AND n.drinks_USD < 15)]->(m {id: 8})
RETURN path;

Additionally, the filter can use the current path of traversal. The filter is defined as a lambda function over r, n, and p, which denotes the relationship expanded over, the node expanded to and the path already collected in the depth-first search.

In the following example, expansion is allowed over relationships with an eu_border property equal to false, to nodes with a drinks_USD property less than 15 and relationship type not equal to CloseTo:

MATCH path=(n {id: 0})-[* (r, n, p | r.eu_border = false AND n.drinks_USD < 15 AND type(last(relationships(p))) != 'CloseTo')]->(m {id: 8})
RETURN path;

Breadth-first search

In breadth-first search (BFS) traversal starts from a single node, and the order of visited nodes is decided based on nodes' breadth (distance from the source node). This means that when a certain node is visited, it can be safely assumed that all nodes that are fewer relationships away from the source node have already been visited, resulting in the shortest path from the source node to the newly visited node.

BFS in Memgraph has been implemented based on the relationship expansion syntax. There are a few benefits of the breadth-first expansion approach, instead of a specialized function. For one, it is possible to inject expressions that filter nodes and relationships along the path itself, not just the final destination node. Furthermore, it's possible to find multiple paths to multiple destination nodes. Also, it is possible to simply go through a node's neighborhood in breadth-first manner.

Currently, it isn't possible to get all the shortest paths to a single node using Memgraph's breadth-first expansion. Unlike DFS, BFS returns only one shortest path.

Below is an example of running the BFS on a simple dataset. The output of the algorithm is one shortest path between the given start and end node found with the breadth-first search traversal.

When to use BFS?

BFS is ideal for finding the shortest path between two nodes in an unweighted graph or between the start node and any other node in the graph. Since it traverses all nodes at a given depth before moving to the next level, it ensures that the shortest path is found.

Getting various results

The following query will show the shortest path between nodes n and m as a graph result.

MATCH path=(n {id: 0})-[*BFS]->(m {id: 8})
RETURN path;

To get the list of relationships, add a variable before the *BFS and return it as a result:

MATCH (n {id: 0})-[relationships *BFS]->(m {id: 8})
RETURN relationships;

To get a list of path nodes use the nodes() function. You can then return the results as a list, or use the UNWIND clause to return individual node properties:

MATCH path=(n {id: 0})-[*BFS]->(m {id: 8})
RETURN nodes(path);

Filtering by relationships type and direction

You can filter relationships by type by defining the type after the relationship list variable, and you decide the direction by adding or removing an arrow from the dash.

In the following example, the algorithm will traverse only across CloseTo type of relationships regardless of the direction:

MATCH (n {id: 0})-[relationships:CloseTo *BFS]-(m {id: 8})
RETURN relationships;

Constraining the path's length

The constraints on the path length are defined after the *BFS. The following query will return a result only if the path is equal to or shorter than 5 hops:

MATCH (n {id: 0})-[relationships:CloseTo *BFS ..5]->(m {id: 8})
RETURN relationships;

The result will be returned only if the path is equal to or longer than 3, and equal to or shorter than 5 hops:

MATCH (n {id: 0})-[relationships:CloseTo *BFS 3..5]-(m {id: 15})
RETURN relationships;

Constraining the expansion based on property values

Breadth-first expansion allows an arbitrary expression filter that determines if an expansion is allowed over a certain relationship to a certain node. The filter is defined as a lambda function over r and n, which denotes the relationship expanded over and node expanded to in the breadth-first search.

In the following example, expansion is allowed over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15:

MATCH path=(n {id: 0})-[*BFS (r, n | r.eu_border = false AND n.drinks_USD < 15)]-(m {id: 8})
RETURN path;

Additionally, the filter can use current path of traversal. To use it the filter is defined as a lambda function over r, n and p, which denotes the relationship expanded over, the node expanded to and the already collected path in the breadth-first search.

In the following example, expansion is allowed over relationships with an eu_border property equal to false, to nodes with a drinks_USD property less than 15 and relationship type not equal to CloseTo:

MATCH path=(n {id: 0})-[*BFS (r, n, p | r.eu_border = false AND n.drinks_USD < 15 AND type(last(relationships(p))) != 'CloseTo')]->(m {id: 8})
RETURN path;

Constraining the expansion based on the number of hops

Overview

Breadth-First Search (BFS), Depth-First Search (DFS), and expand query traversals can now be controlled by the number of hops (edges crossed). Each unit of traversal, including filtering on edge types, edge properties, or visiting already processed nodes, is counted as a hop.

Syntax Usage

The USING HOPS LIMIT x syntax is implemented as a query directive, similar to Index Hints. Users can apply the hops limit as follows:

USING HOPS LIMIT x ...;

The hops limit is global for the entire query and can only be defined once. If you need to use both index hints and a hops limit, the directives can be chained:

USING HOPS LIMIT x, :Label(property) ...;

Implementation Variations

Controlling Partial Results

By default, Memgraph will return partial results after the hops limit is reached. To control the retrieval of partial results, there is a runtime flag available:

hops_limit_partial_results

If this value is set to false and the hops limit is reached, an exception will be thrown.

Example Usage

Let's consider the next graph:

To simplify the expansion process, we will create an index:

CREATE INDEX ON :Node(name);

Now, let's try to find a path between Node A and Node D using the BFS. Running:

USING HOPS LIMIT 2 MATCH path=(start:Node {name: 'A'})-[:ConnectedTo *BFS]->(end:Node {name: 'D'}) RETURN path;

The result is:

Empty set (0.001 sec)

That is because the Node D is not reachable to Node A within 2 hops.

Let's increase the limit to 3 and see what happens:

USING HOPS LIMIT 3 MATCH path=(start:Node {name: 'A'})-[:ConnectedTo *BFS]->(end:Node {name: 'D'}) RETURN path;

+---------------------------------------------------------------------------------------------+
| path                                                                                        |
+---------------------------------------------------------------------------------------------+
| (:Node {name: "A"})-[:ConnectedTo]->(:Node {name: "B"})-[:ConnectedTo]->(:Node {name: "D"}) |
+---------------------------------------------------------------------------------------------+

Now, a path is returned and we see that the Node D is reachable to Node A within the 3 hops using the BFS.

Weighted shortest path

In graph theory, the weighted shortest path problem is the problem of finding a path between two nodes in a graph such that the sum of the weights of relationships connecting nodes, or the sum of the weight of some node property on the path, is minimized.

One of the most important algorithms for finding weighted shortest paths is Dijkstra's algorithm. In Memgraph it has been implemented based on the relationship expansion syntax.

In the brackets following the *WSHORTEST algorithm definition, you need to define what relationship or node property carries the weight, for example, [*WSHORTEST (r, n | r.weight)].

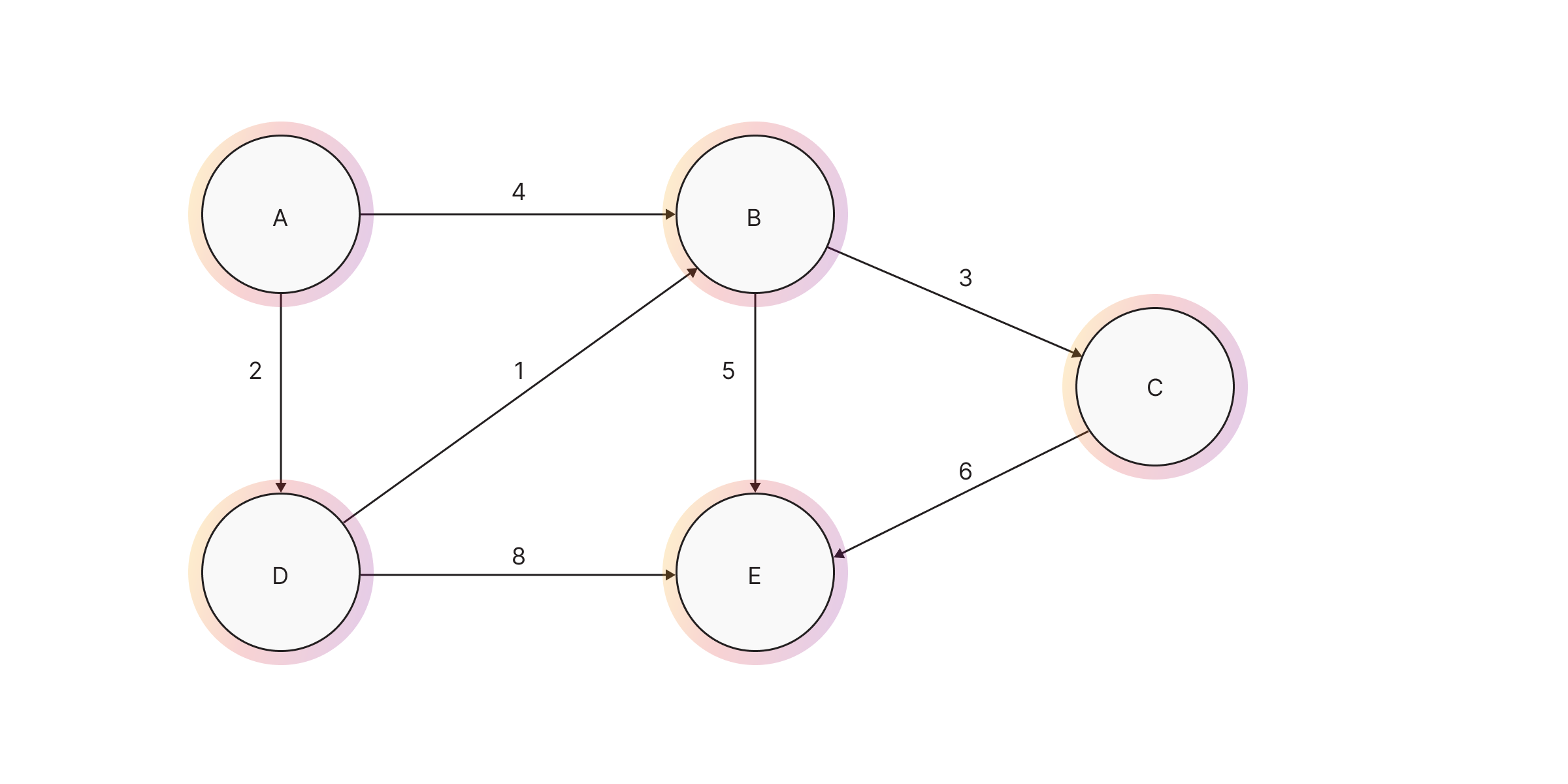
Below is an example of running the WSHORTEST on a simple dataset. The output of the algorithm is one path between the given start and end node with the lowest sum of property weight.

When to use WSP?

Use the weighted shortest path algorithm when you need to find the shortest path between two nodes in a graph with weighted edges. This is particularly useful in scenarios where the cost or distance between nodes varies, such as road networks (where edges represent distances or travel times) or communication networks (where edges represent latency or cost).

When the goal is to optimize a specific metric along the path (e.g., minimizing cost, maximizing profit), a weighted shortest path algorithm can help find the path that optimizes that metric.

Getting various results

To find the weighted shortest path between nodes based on the value of the total_USD node property, traversing only across CloseTo relationships and return the result as a graph, use the following query:

MATCH path=(n {id: 0})-[:CloseTo *WSHORTEST (r, n | n.total_USD)]-(m {id: 15})
RETURN path;

In the above example, the weight is a property of a node, but you can also use weight of some relationship property:

MATCH path=(n {id: 0})-[:Type *WSHORTEST (r, n | r.weight)]-(m {id: 9})
RETURN path;

To get the list of relationships, add a variable before the *WSHORTEST and return it as a result:

MATCH (n {id: 0})-[relationships:CloseTo *WSHORTEST (r, n | n.total_USD)]-(m {id: 9})
RETURN relationships;

To get the path nodes, use the nodes() function. You can then return the results as a list, or use the UNWIND clause to return individual node properties:

MATCH path=(n {id: 0})-[relationships:CloseTo *WSHORTEST (r, n | n.total_USD)]-(m {id: 9})
UNWIND (nodes(path)) AS node
RETURN node.id;

To get the total weight, add a variable at the end of the expansion expression:

MATCH path=(n {id: 0})-[relationships:CloseTo *WSHORTEST (r, n | n.total_USD) total_weight]-(m {id: 9})
RETURN nodes(path), total_weight;

If the weight is taken from the node property and relationship property, the coalesce() function must be used with the relationship property, because when Memgraph calculates the weight of the first node, there is no relationship in the calculation. For example,

MATCH path=(n {id: 0})-[relationships:CloseTo *WSHORTEST (r, n | n.total_USD + coalesce(r.weight, 0)) total_weight]-(m {id: 9})
RETURN nodes(path), total_weight;

Filtering by relationships type and direction

You can filter relationships by type by defining the type after the relationship list variable, and you decide the direction by adding or removing an arrow from the dash.

In the following example, the algorithm will traverse only across CloseTo type of relationships:

MATCH path=(n {id: 0})-[relationships:CloseTo *WSHORTEST (r, n | n.total_USD)]->(m {id: 46})
RETURN relationships;

Constraining the path's length

Memgraph's implementation of the Dijkstra's algorithm uses a modified version of this algorithm that can handle length restriction and is based on the relationship expansion syntax. The length restriction parameter is optional, and when it's not set, it can increase the complexity of algorithm execution. It is important to note that the term "length" in this context denotes the number of traversed relationships and not the sum of their weights.

The following example will find the shortest path with a maximum length of 4 relationships between nodes n and m.

MATCH path=(n {id: 0})-[:CloseTo *WSHORTEST 4 (r, n | n.total_USD) total_weight]-(m {id: 46})
RETURN path,total_weight;

Constraining the expansion based on property values

Weighted shortest path expansion allows an arbitrary expression filter that determines if an expansion is allowed over a certain relationship to a certain node. The filter is defined as a lambda function over r and n, which denotes the relationship expanded over and node expanded to in finding the weighted shortest path.

In the following example, expansion is allowed over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15:

MATCH path=(n {id: 0})-[*WSHORTEST (r, n | n.total_USD) total_weight (r, n | r.eu_border = false AND n.drinks_USD < 15)]-(m {id: 46})
RETURN path,total_weight;

Additionally, the filter can use the current path of traversal and the current weight of the path. The filter is then defined as a lambda function over r, n, p, and w, which denotes the relationship expanded over, the node expanded to, the already collected path and the current weight of the path in the weighted shortest path.

In the following example, expansion is allowed over relationships with an eu_border property equal to false, to nodes with a drinks_USD property less than 15, relationship type not equal to CloseTo and weight less than 1000:

MATCH path=(n {id: 0})-[*WSHORTEST (r, n | n.total_USD) total_weight (r, n, p, w | r.eu_border = false AND n.drinks_USD < 15 AND type(last(relationships(p))) != 'CloseTo' AND w < 1000)]->(m {id: 46})
RETURN path, total_weight;

All shortest paths

Finding all shortest paths is an expansion of the weighted shortest paths problem. The goal of finding the shortest path is obtaining any minimum sum of weights on the path from one node to the other. However, there could be multiple identical-weighted paths, and this algorithm fetches them all.

Weighted shortest path implementation returns only one resulting path from one node to the other. Commonly, multiple shortest paths are flowing through different routes. Syntax of obtaining all shortest paths is similar to the weighted shortest path and boils down to calling [*ALLSHORTEST (r, n | r.weight)] where r and n define the current expansion relationship and node respectively.

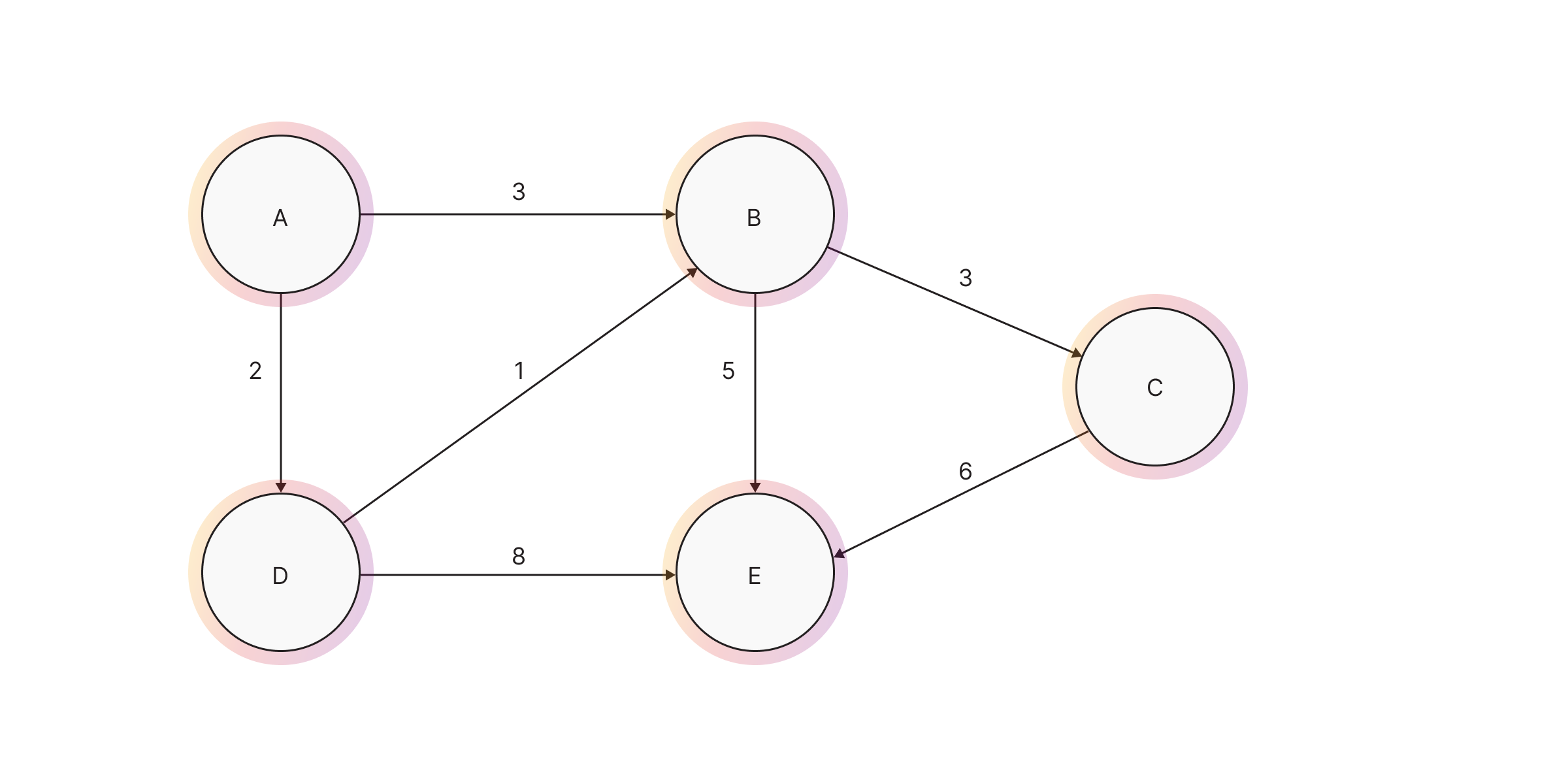
Below is a similar example to the one given previously for the weighted shortest path algorithm, but this time two paths have the same minimum sum of weights since we changed the weight between the nodes A and B.

The output of the algorithm are all paths between the given start and end node with the lowest sum of property weight.

When to use ASP?

Use the all shortest paths algorithm when you need to find all shortest paths between nodes in a graph with weighted edges. This is useful when you need to analyze the network structure or when there may be multiple identical shortest paths between pairs of nodes with minimum cost.

Getting various results

The following query searches for all shortest paths with a default weight equal to 1:

To showcase the characteristics of all shortest paths, we'll use a default weight equal to 1 in the next example.

MATCH path=(n {id: 0})-[:CloseTo *ALLSHORTEST (r, n | 1)]-(m {id: 15})
RETURN path;

The query returns multiple results, all with 4 hops meaning that there are multiple paths flowing from the source node to the destination node.

The following is a weighted query based on the weight property on each visited relationship:

MATCH path=(n {id: 0})-[:Type *ALLSHORTEST (r, n | r.weight)]-(m {id: 5})
RETURN path;

To obtain all relationship on all shortest paths, use the relationships function, unwind the results, and return unique edges so there is no duplicates in our output:

MATCH path=(n {id: 0})-[relationships:CloseTo *ALLSHORTEST (r, n | n.total_USD)]-(m {id: 51})
UNWIND (relationships(path)) AS edge
RETURN DISTINCT edge;

To get the total weight, add a variable at the end of the expansion expression:

MATCH path=(n {id: 0})-[relationships:CloseTo *ALLSHORTEST (r, n | 1) total_weight]-(m {id: 9})
RETURN nodes(path), total_weight;

When the weight is taken from the node property and relationship property, the coalesce() function must be used with the relationship property. It's required because when Memgraph calculates the weight for the first node, there is no relationship in the calculation.

For example:

MATCH path=(n {id: 0})-[relationships:CloseTo *ALLSHORTEST (r, n | n.total_USD + coalesce(r.weight, 0)) total_weight]-(m {id: 9})
RETURN nodes(path), total_weight;

Constraining the path's length

All shortest paths allows for upper bound path restriction. This addition significantly modifies the outcome of the algorithm if the unrestricted shortest path is obtained from a route with more hops than the set upper bound. Finding the all shortest paths with path restriction boils down to finding the minimum weighted path with a maximum length of upper_bound. Upper bound is set to 4 just after the operator:

MATCH path=(n {id: 0})-[:CloseTo *ALLSHORTEST 4 (r, n | n.total_USD) total_weight]-(m {id: 46})
RETURN path,total_weight;

Constraining the expansion based on property values

All shortest paths algorithm enables the usage of an expansions filter. To define it, you need to write a lambda function with a filter expression over r (relationship) and n (node) variables as parameters.

In the following example, expansion is allowed over relationships with a eu_border property equal to false and to nodes with a drinks_USD property less than 20:

MATCH path=(n {id: 0})-[*ALLSHORTEST (r, n | n.total_USD) total_weight (r, n | r.eu_border = false AND n.drinks_USD < 20)]-(m {id: 46})
RETURN path, total_weight;

Additionally, the filter can use the current path of traversal and the current weight of the path. In that case, the filter is defined as a lambda function over r, n, p, and w, which denotes the relationship expanded over, node expanded to, already collected path and current weight of the path in the all shortest path.

In the following example, expansion is allowed over relationships with an eu_border property equal to false, to nodes with a drinks_USD property less than 20, relationship type not equal to CloseTo and weight less than 1000:

MATCH path=(n {id: 0})-[*ALLSHORTEST (r, n | n.total_USD) total_weight (r, n, p, w | r.eu_border = false AND n.drinks_USD < 20 AND type(last(relationships(p))) != 'CloseTo' AND w < 1000)]->(m {id: 46})
RETURN path, total_weight;