pagerank_online (Enterprise)
From Memgraph 3.0, dynamic graph algorithms became a part of the Memgraph Enterprise license. To use dynamic graph algorithms, you need to enable Memgraph Enterprise license. If you want to know more and learn how this affects you, read our announcement.
Online PageRank is a dynamic algorithm made for calculating PageRank in a graph streaming scenario. Incremental local changes are introduced in the algorithm to prevent users from recalculating PageRank values each time a change occurs in the graph (something is added or deleted).
To make it as fast as possible, the online algorithm is only the approximation of PageRank but carrying the same information - the likelihood of random walk ending in a particular vertex. The work is based on “Fast Incremental and Personalized PageRank”, where authors are deeply focused on providing the streaming experience of a highly popular graph algorithm.
Approximating PageRank is done simply by exploring random walks and calculating
the frequency of a node within all walks. R walks are sampled by using a
random walk with a stopping probability of eps.Therefore, on average, walks
would have a length of 1/eps. Approximative PageRank is based on the formula
below:
RankApprox(v) = X_v / (n * R / eps)Where X_v is the number of walks where the node v appears. The theorem
written in the paper explains that RankApprox(v) is sharply concentrated around
its expectation, which is Rank(v).
| Trait | Value |
|---|---|
| Module type | algorithm |
| Implementation | C++ |
| Graph direction | directed |
| Edge weights | unweighted |
| Parallelism | sequential |
This algorithm is currently running in a sequential manner, but can be parallelized. If you have a use case for parallelizing this algorithm, please contact us over Discord.
Procedures
Online PageRank should be used by executing the procedures in the following way:
-
With the
set()procedure, the PageRank values are calculated on the graph for the first time. This function is also important as it sets the streaming context for this algorithm, so further updates of the graph can result in faster execution. -
To make the incremental flow, set the proper trigger using the
update()function:
CREATE TRIGGER pagerank_trigger
(BEFORE | AFTER) COMMIT
EXECUTE CALL pagerank_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;- Use the
get()procedure to return the resulting values stored in the cache. If the user hasn’t previously runset(), the procedure will also do theset()functionality first in order to initialize the streaming context of this algorithm. - Finally, the
reset()function resets the context and enables you to start new runs.
You can execute this algorithm on graph projections, subgraphs or portions of the graph.
set()
The procedure calculates PageRank for the nodes in the graph. The procedure is currently running in a sequential manner, but can be parallelized (the non-streaming version of pagerank offers parallelism, but is not applicable as it doesn’t set the streaming context for the algorithm).
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.walks_per_node: integer (default=10)➡ Number of sampled walks per node.walk_stop_epsilon: double (default=0.1)➡ The probability of stopping when deriving the random walk. On average, it will create walks of length1 / walk_stop_epsilon.
Output:
node➡ Node in the graph, for which PageRank is calculated.rank➡ Normalized ranking of a node. Expresses the probability that a random surfer will finish in a certain node by a random walk.
Usage:
Use the following query to calculate PageRank:
CALL pagerank_online.set()
YIELD node, rank;get()
The get() procedure is used if the trigger has been set or a set() procedure
has been called, before adding changes to the graph.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.
Output:
node➡ Node in the graph, for which PageRank is calculated.rank➡ Normalized ranking of a node. Expresses the probability that a random surfer will finish in a certain node by a random walk.
Usage:
Use the following query to get the PageRank values:
CALL pagerank_online.get()
YIELD node, rank
RETURN node, rank;update()
The procedure recalculates the values of the PageRank based on the recent changes in the graph.
Input:
subgraph: Graph(OPTIONAL) ➡ A specific subgraph, which is an object of type Graph returned by theproject()function, on which the algorithm is run. If subgraph is not specified, the algorithm is computed on the entire graph by default.created_vertices➡ Nodes that were created in the last transaction.created_edges➡ Relationships created in a period from the last transaction.deleted_vertices➡ Nodes deleted from the last transaction.deleted_edges➡ Relationships deleted from the last transaction.
Output:
node➡ Node in the graph, for which PageRank is calculated.rank➡ Normalized ranking of a node. Expresses the probability that a random surfer will finish in a certain node by a random walk.
Usage:
Use the following query to set a trigger to recalaculate the PageRank values after changes to the graph:
CREATE TRIGGER pagerank_trigger
(BEFORE | AFTER) COMMIT
EXECUTE CALL pagerank_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;Example
Set parameters
Use the following query to set parameters:
CALL pagerank_online.set(100, 0.2)
YIELD node, rank;Create a trigger
The following query creates a trigger which will update the values upon creating new data or deleting existing data:
CREATE TRIGGER pagerank_trigger
BEFORE COMMIT
EXECUTE CALL pagerank_online.update(createdVertices, createdEdges, deletedVertices, deletedEdges)
YIELD node, rank
SET node.rank = rank;Add new data
New data is added to the database:
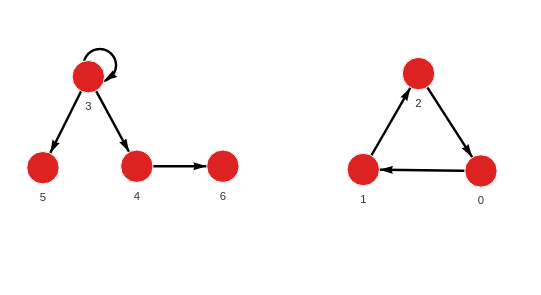
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 3}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 6}) CREATE (a)-[:RELATION]->(b);As new data is added, the triggered pagerank.update() procedure calculates the values.
Get PageRank
Return the values using the following query:
MATCH (node)
RETURN node.id AS node_id, node.rank AS rank;Results:
+-----------+-----------+
| node_id | rank |
+-----------+-----------+
| 0 | 0.225225 |
| 1 | 0.225225 |
| 2 | 0.225225 |
| 3 | 0.0675676 |
| 4 | 0.0765766 |
| 5 | 0.0585586 |
| 6 | 0.121622 |
+-----------+-----------+