Monitoring a Dynamic Contact Network With Online Community Detection

This tutorial is a sequel to LabelRankT – Community Detection in Dynamic Environment.

Introduction

The newest spell in MAGE’s book is Online Community Detection. – an efficient, high-performance algorithm for detecting communities in networks that change with time.

As MAGE wants to use his knowledge to help people, in this tutorial you will learn with him how to build a utility that monitors a dynamic contact network. The utility will a) use the detected communities to show rumor-spreading clusters and b) track the average cluster size.

How did our magician learn about all of this, though?

It was again winter – too soon, MAGE sighed – and something odd was happening with his sage 🧙 friends. They were arguing with one another, and between fights, they were wondering what was up. Soon they found out that rumors had somehow spread among them. Losing no time, MAGE set off to find a way to make sense of the situation with what he knows best – graphs. Having built a network that tracked their close contacts through time, he pored over his books until he found a suitable algorithm for analyzing it. [1]

Prerequisites

To complete this tutorial, you will need:

1. MAGE – Memgraph’s very own graph analytics library
2. gqlalchemy – a Python driver and object graph mapper (OGM)

Graph

It is paramount to protect the privacy of personal contact records. Keeping this in mind, we generated a dynamic dataset (250 nodes and < 1700 vertices) of a network of close contacts using the Barabási–Albert graph generation model. This model is suitable for such networks because it makes graphs with two traits that one commonly sees in real-life networks:

1. small world property: few degrees of separation between any two nodes in the graph
2. power-law degree distribution: the presence of hubs (highly connected nodes) in the graph

Our graph consists of Person nodes with a contactID attached. If two Persons have been in close contact, there exists between them a relationship CONTACTED.

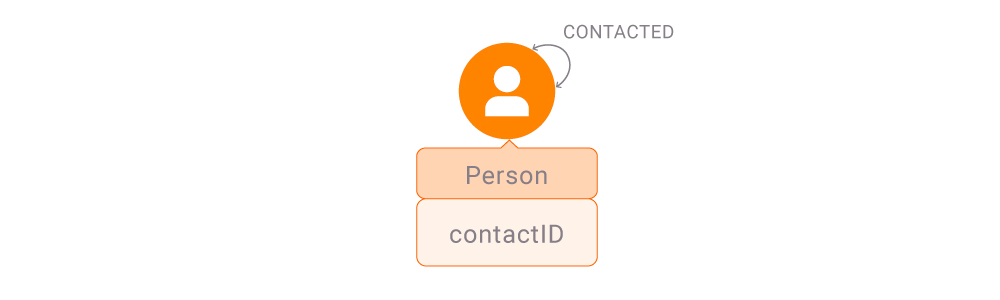
Contacts of age over the rumor’s “expiration date” do not play a role in rumor spreading and are thus dropped. Consequently, this means that communities of close contacts are not static; instead, they change with time, and communities need to be updated after each update anew.

Algorithm

We will do our network analysis with the new LabelRankT method described in the previous post. LabelRankT is an online algorithm that partitions the network into communities and returns nodes with their community labels.

In a nutshell, the algorithm does two main operations:

1. label propagation: assign each node a label and pass them along edges for several iterations
2. update: find the changed nodes and run label propagation on them only
   

Now, why did MAGE use this algorithm?

Let’s remember that we defined communities as sets of densely interconnected nodes. These are what our algorithm detects – as labels flow through the network, the sets quickly converge on a single one.

As for our task, this idea allows us to extend the notion of “close contact” to people who haven’t had direct contact with a rumor spreader if they are sufficiently connected to the people who have. In other words, rumors can quickly spread through the network, much like a chain reaction would. In effect, communities are essentially rumor-spreading clusters. This way, we can cast a wider net and inform more people about possible exposure to misinformation.

Loading the dataset

The dataset is a file whose entries are structured as follows:

+|-,contactID_1,contactID_2

If the initial operator is +, the entry adds a contact between contactID_1 and contactID_2 to the network; - does the opposite.

Memgraph supports graph streaming. When working with a dynamic network, one would usually create a stream and connect it and Memgraph. However, we’re focused on rumor spreading and working with streams is a bit beside the point. Instead, we’ll simulate a stream with this little snippet of code:

class Stream:
    i = 0
    data = [['+',120,954], ...]

    CREATE_EDGE = 'MERGE (a: Person {{contactID: {}}})
                   MERGE (b: Person {{id: {}}})
                   CREATE (a)-[r: CONTACTED]->(b);'
    DELETE_EDGE = 'MATCH (a: Person {{contactID: {}}})-[r: CONTACTED]->(a: Person {{contactID: {}}})
                   DELETE r;'

    def get_next(self):
        if self.i >= len(self.data):
            return None
        operation, node_1, node_2 = *self.data[self.i]
        self.i += 1
        if operation == '+':
            return self.CREATE_EDGE.format(node_1, node_2)
        elif operation == '-':
            return self.DELETE_EDGE.format(node_1, node_2)

Setting up detection

We will need two procedures: set() initializes the community detection algorithm and update() gets the new communities after each graph change.

Initialization with set() should look like the following:

CALL dynamic_community_detection.set()
YIELD node, community_id
RETURN node.id AS node_id, community_id
ORDER BY node_id;

This method lets the user set the parameters of the algorithm, as detailed in the documentation. Note that we are using the default values in this article.

Triggers are a Memgraph functionality that lets users set openCypher statements to run in response to graph updates. We will handle community updating with a trigger that activates after every graph change:

CREATE TRIGGER test_edges_changed
BEFORE COMMIT EXECUTE
CALL dynamic_community_detection.update(
    createdVertices,
    createdEdges,
    updatedVertices,
    updatedEdges,
    deletedVertices,
    deletedEdges) YIELD *;

The arguments passed to update() are predefined within the trigger. For a comprehensive list of trigger events and their predefined variables, take a look here in the documentation.

Putting it all together

Finally, we’re going to put this all together. 🚀

The main loop of our code holds the bulk of our utility’s logic. It handles the tasks of updating the graph, community detection, and returning rumor-spreading clusters and their mean sizes.

memgraph = Memgraph("127.0.0.1", 7687)

example_stream = Stream()
memgraph.execute(query=INIT_ALGORITHM)
memgraph.execute(query=UPDATE_TRIGGER)

while True:
    # update graph and run community detection

    next_change = example_stream.get_next()
    if not next_change:
        break
    memgraph.execute(query=next_change)
    results = memgraph.execute_and_fetch(query=GET_RESULTS)


    # for a random node, find its cluster

    nodes = []
    for result in results:
        node, _ = list(result.values())
        nodes.append(node)

    random_node = random.choice(nodes)
    cluster = []
    for result in results:
        node, community = list(result.values())
        if node == random_node:
            cluster.append(node)


    # calculate mean cluster size

    sizes = {}
    for result in results:
        node, community = list(result.values())
        if community not in sizes.keys():
            sizes[community] = 0
        else:
            sizes[community] += 1
    sizes = list(sizes.values())
    mean_size = sum(sizes) / len(sizes)

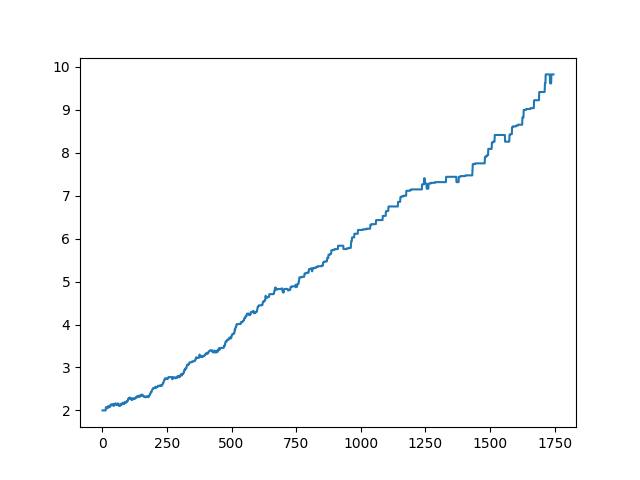
To wrap up this demo, here’s a plot of mean cluster/community size by epoch:

Conclusion

This article aimed to present the efficiency and output quality of MAGE’s new online community detection algorithm on a dynamic network, stressing the insights that one can glean from the communities. With the ongoing rise in data streaming, the demand for algorithms that can handle large volumes of data and produce useful results is rising, and our algorithm is one of them.

Our team of engineers is currently tackling the problem of graph analytics algorithms on real-time data. If you want to discuss how to apply online/streaming algorithms on connected data, feel free to join our Discord server and message us.

MAGE shares his wisdom on a Twitter account. Get to know him better by following him 🐦

Last but not least, check out MAGE and don’t hesitate to give a star ⭐ or contribute with new ideas.

References

[1] Jierui Xie, Mingming Chen, Boleslaw K. Szymanski: “LabelRankT: Incremental Community Detection in Dynamic Networks via Label Propagation”, 2013, Proc. DyNetMM 2013 at SIGMOD/PODS 2013, New York, NY, 2013; arXiv:1305.2006.