LabelRankT – Community Detection in Dynamic Environment
Introduction
Community detection helps us uncover hidden relations among nodes in a graph and find sets of nodes with some characteristics in common. Real-life networks often show community structure, and by figuring it out, one can tackle a wide range of problems.
If you’re doing graph analytics, the chances are that you have run community detection on the dataset. Algorithms take more time to run on large graphs, and handling the volume of work that comes along with a large and frequently updated dataset is an engineering problem. It makes sense to wonder if it’s possible to leverage the small size of an average update to deliver a performance boost.
We at Memgraph recognize your challenges. In this article, you will learn about the merits of online community detection methods and get acquainted with the LabelRankT algorithm by Xie et al., now available in MAGE 1.1.

The case for online algorithms
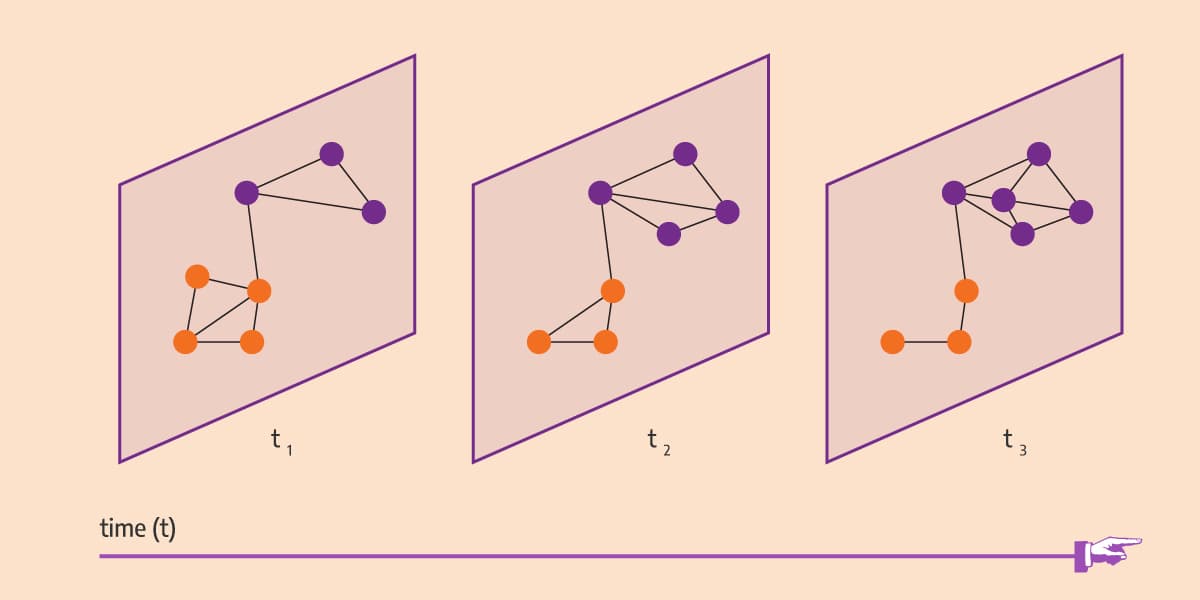
Picture a family or a group of close friends – they feel a strong sense of community to one another, and their mutual relationships run deeper than those with people outside the bunch. Now, let’s say that the family got a new arrival or that a new friend joined the crew. These communities changed, but this doesn’t imply that others did so. In other words, the change was local in scope.
Modern tech operations often work with big data, which is so in more than one way: individual datasets both reach large sizes and receive frequent updates. Scalability means that one needs to cut down on repetition and leverage that updates often change just a tiny piece of the data. One needs online algorithms – methods that process data as it comes.
Community detection lends itself well to online solutions for two reasons:
- Complexity: many methods have high time complexity that scales with the number of nodes in the network
- Locality: community changes tend to be local in scope after partial updates.
Graph streaming platforms such as Memgraph are natively dynamic environments, stressing the need for specialized algorithms on top of the usual performance considerations.
To equip Memgraph with a suitable algorithm, the MAGE team peered into spellbooks academic research and implemented LabelRankT (Xie et al.).
The LabelRankT algorithm
LabelRankT is an un-/semi-supervised machine learning algorithm made for online community detection on networks. It takes a graph as input and returns an assignment of nodes to the communities it detected; nodes belong to a single community. Offline and online modes of operation are both supported; the latter takes advantage of the communities found in the previous iteration of the graph, whereas the former detects them ab initio. The algorithm supports weighted and directed graphs by design.
Concepts
In network science, we define a community as a set of nodes that are densely connected internally.
Label propagation algorithms initialize every node with a unique label, and then these diffuse through the network. Consequently, densely interconnected groups – communities – quickly reach a common label.
Nodes do not wholly belong to a single community under LabelRankT. Instead, every node has an associated label distribution vector composed of label probabilities. The vector is scaled so that the probabilities sum to 1.
A self-loop is added to each node to stabilize the detection results across iterations.
Detection
The algorithm starts by assigning a unique label to every node in the graph. Label distribution vectors are initialized as follows:
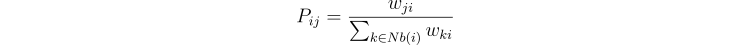
In other words, the probability that node i belongs to community j is the ratio of wⱼᵢ and the total weight of all edges that lead to i.
Label propagation is an iterative process with four steps per iteration. Below follows an abridged description of the steps:
- Node selection: nodes belonging to the same community as at least k/% of their neighbors skip the next three steps
- Label propagation: for an individual node, its new label distribution is a weighted sum of its in-neighbors’ distributions (incl. its own):
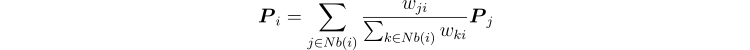
- Inflation: label distribution vectors are raised elementwise to the nth power and then scaled to sum to 1
- Cutoff: label probabilities under a set threshold are pruned.
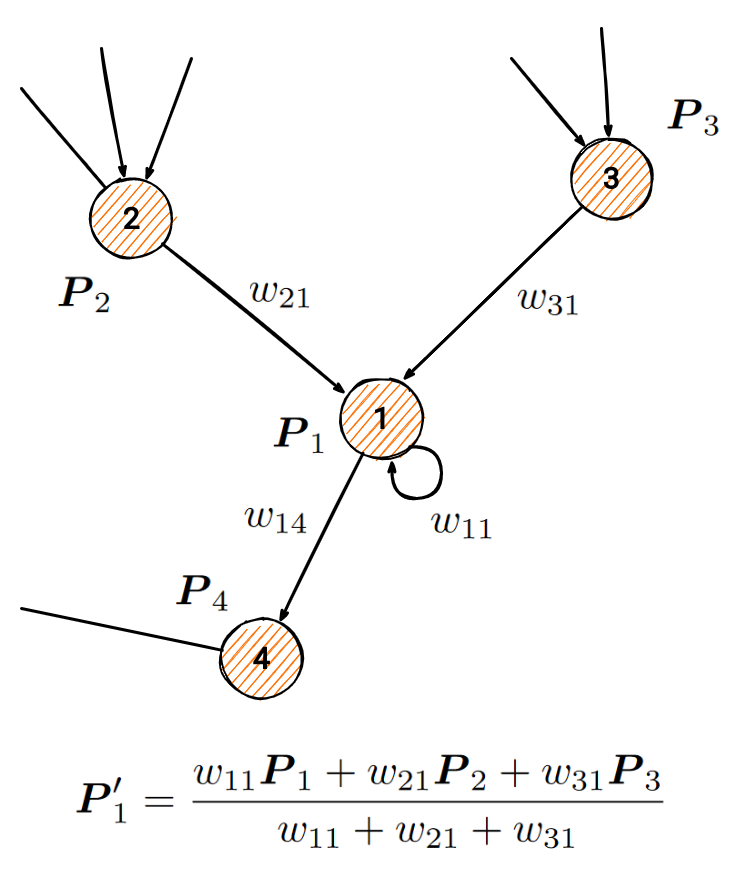
After several iterations, the algorithm converges on a solution and returns the most probable labels for each node.
Node selection passes over nodes whose labels are too much like the neighbors’. In those cases, label propagation is likely not to change anything, and skipping it makes sense due to its expensiveness. The inflation and cutoff steps help optimize the algorithm by cutting down the number of labels stored in the nodes’ label distribution vectors.
Online operation
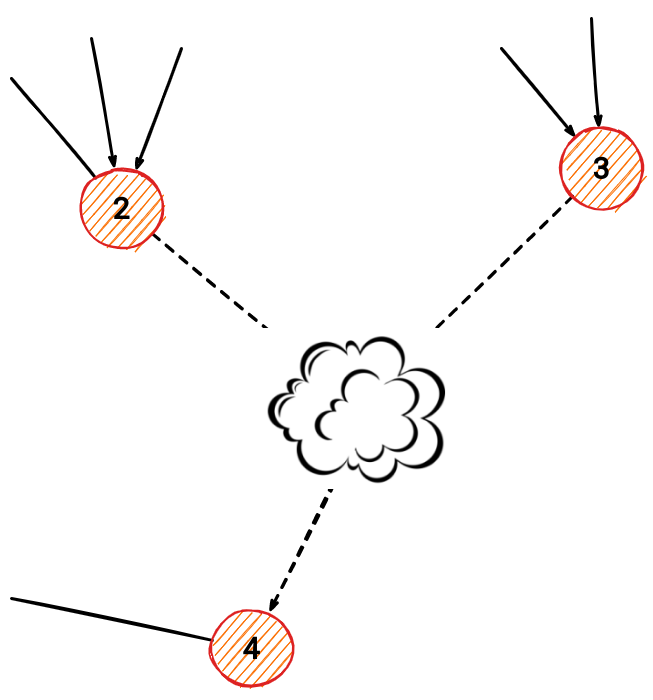
Being an online algorithm, LabelRankT builds its solution incrementally as it adapts to changes in the input. Changed nodes are defined as all nodes that have been added, edited, or deleted, as well as their neighbors. If an edge has been added, edited, or deleted, its endpoint nodes are also considered to be changed.
Compared to the mathematical operations described in the previous section, the logic of online operation is simple:
- Find out which nodes are changed
- Preserve the community labels of unchanged nodes
- Re-run community detection on changed nodes only
Performance
LabelRankT runs in linear O(m) time and takes O(mn) space on a graph with n nodes and m edges. Total execution time also depends on the number of iterations set for label propagation.
This section assesses the performance of LabelRankT on two dimensions: we compare offline community detection methods against offline ones in general and contrast LabelRankT’s properties with those of other community detection algorithms.
Online methods
➕ much faster on large, dynamic graphs than offline methods
➕ adaptive to changes in the input data
➖ assumption that the changes only have local effects
➖ need to store past state(s) in memory
LabelRankT
➕ result quality matching offline algorithms
➕ low computational cost
➕ scalable to very large graphs
➕ deterministic and replicable results (unlike other label propagation methods)
➕ compatible with directed and weighted graphs
➕ customizable parameters
➖ less grounded in theory than statistical and modularity-maximizing algorithms for community detection
Applications
Graphs that describe real-life networks show community structure often.
This insight applies to diverse use cases such as customer segmentation, contact tracing, medical diagnostics, and quantification of environmental hazards in public health. As communities often correspond to the functional units of systems, additional use cases include the detection of cycles or pathways in metabolic networks and recommender systems where content forms communities sorted by topic. Furthermore, tracking the evolution of communities across time provides a way to monitor entities such as viruses or rumors in real-time as they spread. With the COVID-19 pandemic being a top global concern, this problem is in search of a solution.
In all cases, online methods are well-suited for frequently updated graphs as they save time by re-running the detection only on changed nodes.
A key property of communities is that they often have very different properties than the rest of the network. If one knows the division of the graph into communities, it is possible to isolate them for closer study. Conversely, this can allow one to treat entire communities as single meta-nodes, effectively reducing the size of the graph and allowing analysis with complex methods that otherwise wouldn’t scale – big data turned small!
Communities detected by LabelRankT have a quality that matches traditional offline algorithms. Being deterministic, the algorithm is also suitable for scientific applications that call for replicability.
Conclusion
Community detection is a common task in graph analytics owing to its wide variety of applications, but in big data, it faces concerns on the grounds of scalability in dynamic environments. Online methods such as LabelRankT help solve this by saving previously calculated results in unchanged graph regions.
Our team of engineers is currently tackling the problem of graph analytics algorithms on real-time data. If you want to discuss how to apply online/streaming algorithms on connected data, feel free to join our Discord server and message us.
MAGE shares his wisdom on a Twitter account. Get to know him better by following him 🐦
Last but not least, check out MAGE and don’t hesitate to give a star ⭐ or contribute with new ideas.