Memgraph’s Deep Path Traversal Capabilities

By Matea Pesic

16 min readApril 24, 2024

Let’s explore Memgraph deep path traversal algorithms, how they work, and how they enhance query processing and boost performance in large-scale graph environments.

In contrast to other graph databases, Memgraph deep path traversals efficiently handle complex graph queries, as these algorithms have been built into Memgraph's core. This eliminates the need for the overhead of business logic on the application side.

Types of Deep Path Traversals

There are four built-in deep path traversal algorithms in Memgraph:

Check out our Graph algorithms infographic for a visual overview of these advanced algorithms and others that can further enhance your graph query processing.

We’ll dive deep into each of these and give optimization solutions.

Depth-First Search

The DFS algorithm starts at the root node and explores each neighboring node as far as possible. The moment it reaches a dead-end, it backtracks until it finds a new, undiscovered node, then traverses from that node to find more undiscovered nodes. In that way, the algorithm visits each node in the graph.

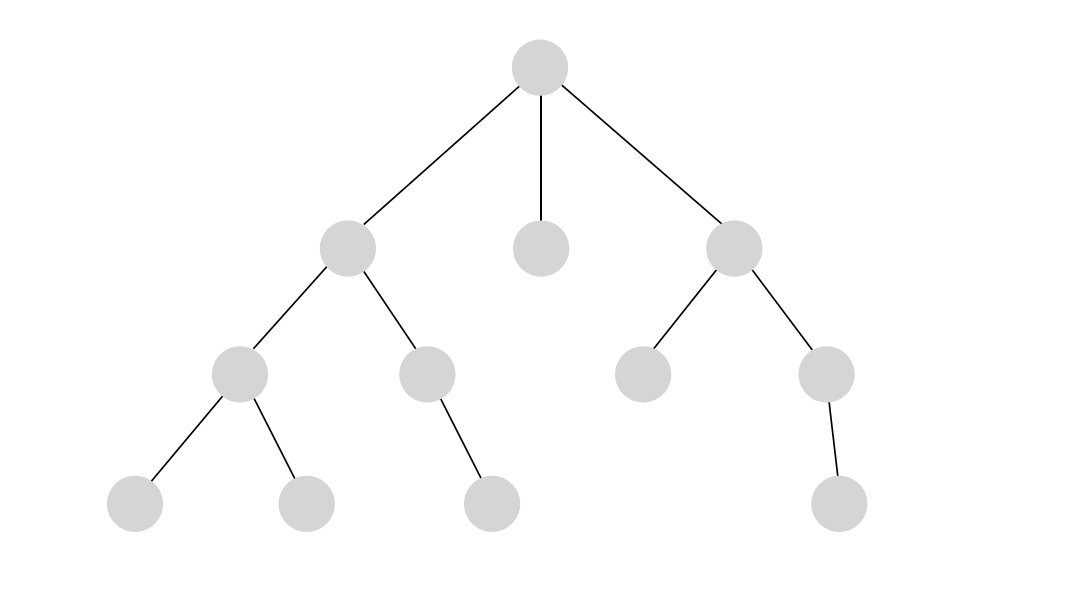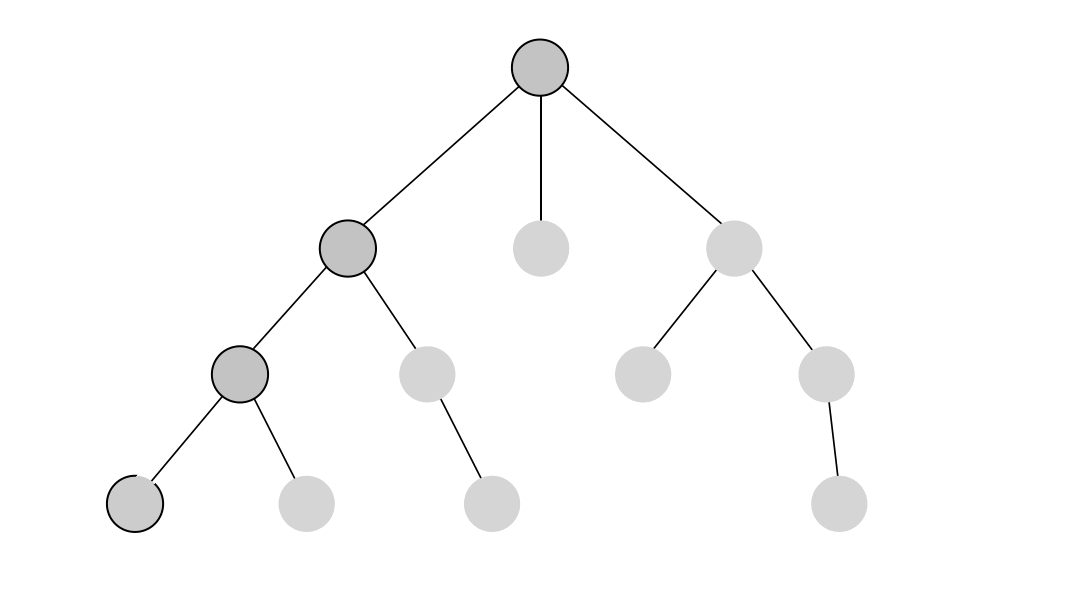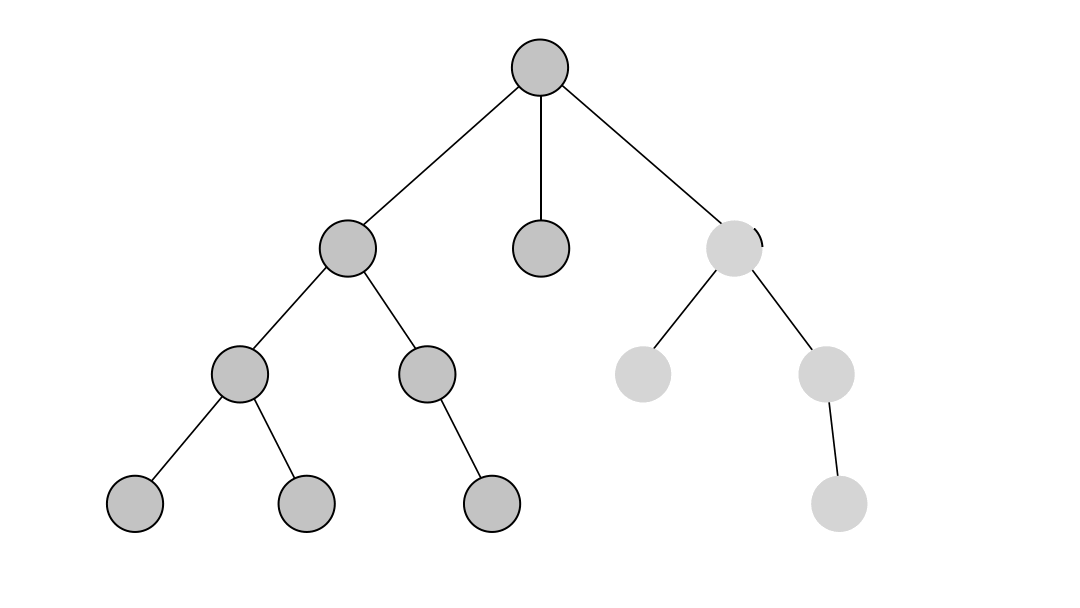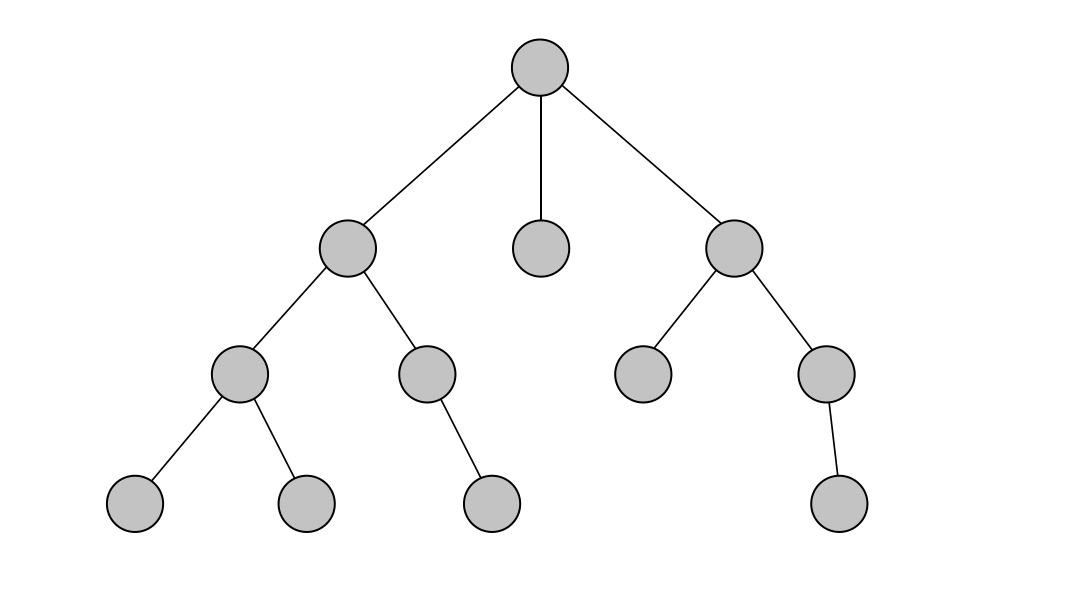
Using DFS

DFS returns all the paths found between given nodes and is the most suitable for determining the existence of paths between two nodes in a graph. If the algorithm's output is null, no paths are available between the nodes. The DFS algorithm will provide all possible paths if the output is not null.

The following query will show all the paths from node n to node m:

MATCH path=(n {id: 0})-[*]->(m {id: 8})
RETURN path;

You can filter relationships by type by defining the type after the relationship list variable. You decide the direction by adding or removing an arrow from the dash, constrain the path length and constrain the expansion based on property values.

The following query showcases all three possibilities. It allows traversal only across CLOSE_TO relationship type, it limits the path length to 5 hops and the expansion is allowed over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15:

MATCH path=(n {id: 0})-[r:CLOSE_TO *..5 (r, n | r.eu_border = false AND n.drinks_USD < 15)]->(m {id: 8})
 
RETURN path;

Breadth-First Search

In BFS, traversal starts from a single node, and the order of visited nodes is decided based on nodes' breadth (distance from the source node). When we visit a particular node, we can safely assume that all the nodes which are closer to the source node have already been visited. This results in finding the shortest path from the source node to the newly visited node.

Using BFS

BFS is ideal for finding the shortest path between two nodes in an unweighted graph or between the start node and any other node in the graph. Since it traverses all nodes at a given depth before moving to the next level, it ensures that the shortest path is found.

The following query will show the shortest path between nodes n and m:

MATCH path=(n {id: 0})-[*BFS]->(m {id: 8})
RETURN path;

Similar to DFS, with BFS you can also filter relationships by type, constrain the path length and constrain expansion based on the property values.

The following query showcases all the mentioned possibilities. It allows traversal only across CLOSE_TO relationship type, it limits the path length to from 3 to 5 hops and the expansion is allowed over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15:

 
MATCH path=(n {id: 0})-[r:CLOSE_TO *BFS 3..5 (r, n | r.eu_border = false AND n.drinks_USD < 15)]->(m {id: 8})
 
RETURN path;

Weighted Shortest Path

In graph theory, the weighted shortest path problem is the problem of finding a path between two nodes in a graph such that the sum of the weights of relationships connecting nodes, or the sum of the weight of some node property on the path, is minimized.

weighted shortest path

Using WSP

Use the weighted shortest path algorithm to find the shortest path between two nodes in a graph with weighted edges. This is particularly useful in scenarios where the cost or distance between nodes varies, such as road networks (where edges represent distances or travel times) or communication networks (where edges represent latency or cost).

When the goal is to optimize a specific metric along the path (e.g., minimizing cost, maximizing profit), a weighted shortest path algorithm can help find the path that optimizes that metric.

To find the weighted shortest path between nodes based on the value of the total_USD node property, traversing only across CLOSE_TO relationships and returning the result as a graph, use the following query:

 
MATCH path=(n {id: 0})-[:CLOSE_TO *WSHORTEST (r, n | n.total_USD)]-(m {id: 15})
 
RETURN path;

To find the weighted shortest path between nodes based on the value of the total_USD node property, traversing only across CLOSE_TO relationships with a maximum length of 5 relationships while allowing the expansion only over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15 use the following query:

 
MATCH path=(n {id: 0})-[:CLOSE_TO *WSHORTEST 5 (r, n | n.total_USD) total_weight (r, n | r.eu_border = false AND n.drinks_USD < 15)]-(m {id: 46})
 
RETURN path,total_weight;

All Shortest Paths

Finding all shortest paths is an expansion of the weighted shortest paths problem. The goal of finding the shortest path is obtaining any minimum sum of weights on the path from one node to the other. However, there could be multiple similar-weighted paths, and this algorithm fetches them all.

Using ASP

Use the all shortest paths algorithm to find all shortest paths between nodes in a graph with weighted edges. This is useful when you need to analyze the network structure or when there may be multiple identical shortest paths between pairs of nodes with minimum cost.

The following query searches for all shortest paths with a default weight equal to 1:

 
MATCH path=(n {id: 0})-[:CloseTo *ALLSHORTEST (r, n | 1)]-(m {id: 15})
 
RETURN path;

To find the all shortest paths between nodes based on the value of the total_USD node property, traversing only across CLOSE_TO relationships with maximum length of 5 relationships while allowing the expansion only over relationships with an eu_border property equal to false and to nodes with a drinks_USD property less than 15 use the following query:

 
MATCH path=(n {id: 0})-[:CLOSE_TO *ALLSHORTEST 5 (r, n | n.total_USD) total_weight (r, n | r.eu_border = false AND n.drinks_USD < 15)]-(m {id: 46})
 
RETURN path,total_weight;

Optimizing Graph Traversals

Optimizing traversal algorithms can significantly enhance performance in Memgraph, especially when dealing with large datasets. Techniques like creating indexes, filtering by relationship type, and constraining path lengths can help streamline queries and reduce execution time.

Here’s an example of how you can optimize a traversal to find all cities connected to London through the shortest road paths using BFS. We'll find all shortest paths from the starting node with the name property being London to all of the nodes in the dataset.

 
MATCH path=(:City {name: 'London'})-[*BFS]->(:City)
 
RETURN path;

This query returns nodes representing cities London is connected to with the transportation network. Since we didn't provide any restrictions and filtering, the algorithm scans and traverses through the entire dataset which can lead to slower performance on larger-scale datasets.

Creating Indexes

Creating indexes on relevant properties can drastically speed up traversal queries by shortening the database scanning time. In Memgraph, indexes can be created using Cypher queries like:

 
CREATE INDEX ON :Node(property)

This query creates an index on the property of nodes, enabling faster lookups during algorithm traversals.

Filtering by Relationship Type

Unlike other graph databases, Memgraph supports inline filtering, enabling efficient traversal through graph structures. This approach allows for precise control over how relationships are traversed, including filtering by type and the direction of the relationship, avoiding subsequent filtering using the WHERE clause.

Let's take the same example from above, but this time limiting traversal across roads only, eliminating other types of transportation. In other words, we'll provide a relationship type filter to the previously used query and limit it only to traverse through the relationship type ROAD.

 
MATCH path=(:City {name: 'London'})-[r:ROAD *BFS]->(:City)
 
RETURN path;

This way, Memgraph eliminates traversing through unnecessary relationships, shortening the execution time.

Filtering by Property Value

Traversal algorithms allow an expression filter that determines if an expansion is allowed over a certain relationship or node property value.

Let's take the same example from above, but this time limiting traversal through the European roads only. We want to apply filters to the relationship property continent and set the value to exactly Europe.

 
MATCH path=(:City {name: 'London'})-[r:ROAD *BFS (r, n | r.continent = 'Europe')]->(:City)
 
RETURN path;

This way, Memgraph eliminates traversing through unnecessary relationships and property values, shortening the execution time even more.

Constraining Path Length

By constraining the length of the path, the algorithm won't do unnecessary scanning and return results after finding results with the maximum number of hops.

The following query will only return the results if the path is equal to or shorter than 2 hops:

 
MATCH path=(:City {name: 'London'})-[r:ROAD *BFS ..2 (r, n | r.continent = 'Europe')]->(:City)
 
RETURN path;

By knowing your dataset's schema and filtering and limiting the wanted results, you can achieve a much more optimized way of using the traversal algorithms.

Conclusion

Unlike many graph databases that rely on external libraries or plugins for deep path traversals, Memgraph integrates these algorithms directly into the core system. This direct integration means less overhead and better performance. The traversals can take full advantage of Memgraph’s internal optimizations and architecture.

The variety of supported algorithms—DFS, BFS, WSP, and ASP—allows users to tailor their graph queries to the specific demands of their data and use case scenarios.

Additionally, Memgraph's support for advanced query optimization techniques, such as creating indexes, filtering by relationship type or property values, and constraining path lengths, empowers developers to fine-tune their queries for maximum performance. These capabilities are essential for exploring and analyzing large-scale graph data efficiently and can unlock deeper insights into complex datasets.

For developers and data scientists looking for a robust, scalable, and efficient solution for graph data management, Memgraph offers a compelling platform that enhances both the development experience and the analytical capabilities of your applications. Whether you are working on real-time recommendation systems, network analysis, or complex routing problems, Memgraph's powerful traversal and optimization features are designed to meet your needs. Start leveraging these advanced capabilities in Memgraph today to drive your graph-based projects toward more innovative and performant outcomes.