Understanding Cosine Similarity in Python with Scikit-Learn
Cosine similarity proved useful in many different areas, such as in machine learning applications, natural language processing, and information retrieval. After reading this article, you will know precisely what cosine similarity is, how to run it with Python using the scikit-learn library (also known as sklearn), and when to use it. You’ll also learn how cosine similarity is related to graph databases, exploring the quickest way to utilize it.
Cosine similarity algorithm: Deep dive
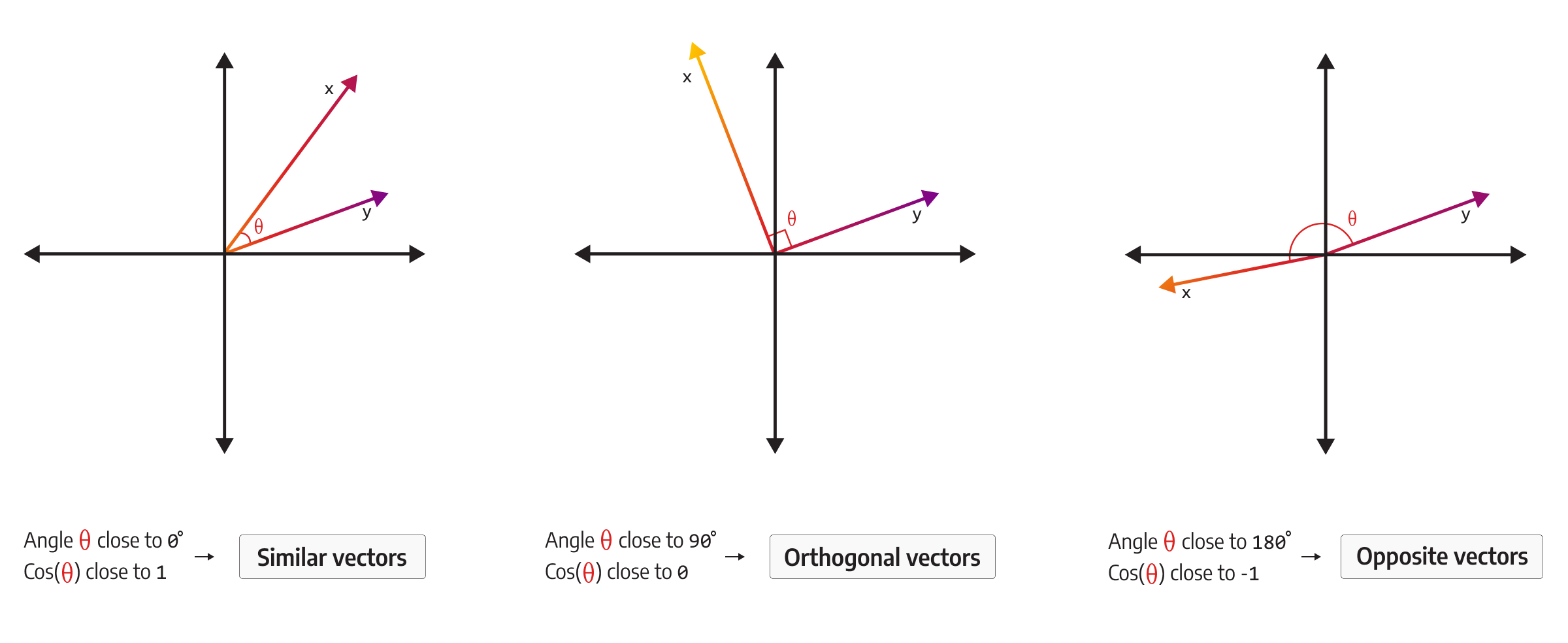
Cosine similarity is a measure of similarity between two non-zero vectors of an inner product space based on the cosine of the angle between them, resulting in a value between -1 and 1. The value -1 means that the vectors are opposite, 0 represents orthogonal vectors, and value 1 signifies similar vectors.
The cosine similarity formula
To compute the cosine similarity between vectors A and B, you can use the following formula:
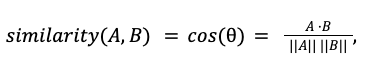
Here is the angle between the vectors, AB is the dot product between A and B, while A and B are the magnitudes, or lengths, of vectors A and B, respectively. The dot product can be expressed as a sum of the product of all vector dimensions and magnitudes as:
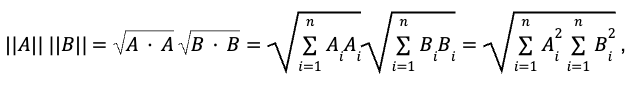
So the cosine similarity formula is equivalent to:
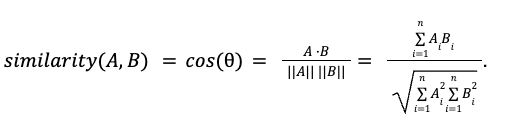
The cosine similarity is often used in text analytics to compare documents and determine if they’re similar and how much. In that case, documents must be represented as a vector, where a unique word is a dimension and the frequency or weight of that unique word in the document represents the value of that specific dimension. After the transformation of documents to vectors is done, comparison using cosine similarity is relatively straightforward — we measure the cosine of the angle between their vectors. If the angle between vectors (documents) is small, then the cosine of the angle is high, and hence, documents are similar. Opposite to that, if the angle between vectors (documents) is large, then the cosine of the angle is low, resulting in opposite documents (not similar). Cosine similarity considers the orientation of the vectors, but it does not take their magnitudes into account. In the previous example, this means that even documents of totally different lengths can be considered similar if they are related to the same topic.
Exploring Python libraries for cosine similarity
As explained in the previous chapter, cosine similarity can be easily calculated using the mathematical formula. But what if the data you have becomes too large and you want to calculate the similarities fast? The most popular programming language used for such tasks is definitely Python and its flexibility is partly due to its extensive range of libraries. For calculating cosine similarity, the most popular ones are:
- NumPy: the fundamental package for scientific computing in Python, which has functions for dot product and vector magnitude, both necessary for the cosine similarity formula.
- SciPy: a library used for scientific and technical computing. It has a function that can calculate the cosine distance, which equals 1 minus the cosine similarity.
- Scikit-learn: offers simple and efficient tools for predictive data analysis and has a function to directly and efficiently compute cosine similarity.
From the above-mentioned libraries, only scikit-learn directly calculates the cosine similarity between two vectors or matrices, making it an excellent tool for data analysts and machine learning enthusiasts. It provides sklearn.metrics.pairwise.cosine_similarity function to do that, and we will show how it works on an example
How to calculate cosine similarity
To demonstrate how to calculate cosine similarity in a simple example, let’s take the descriptions of the most popular social networks from Wikipedia and compare them. The library used for calculating cosine similarity is scikit-learn, as mentioned in the previous section since it calculates cosine similarity directly with the help of sklearn.metrics.pairwise.cosine_similarity function. Besides that function, CountVectorizer from scikit-learn is used to convert the collection of text documents into a matrix of token counts. CountVectorizer has attribute stop_words which can be used to avoid counting most common words in English text, such as “and,” “the,” and “him,” which are presumed to be uninformative in representing the content of the text and which should be removed to avoid them being used in measuring similarity between two texts. Sometimes, these words are good to have to compare someone’s writing style or personality. Here is the code used to calculate the similarity between Twitter, Facebook, TikTok, and Instagram:
from sklearn.feature_extraction.text import CountVectorizer
import pandas as pd
from sklearn.metrics.pairwise import cosine_similarity
twitter = """
Twitter is an online social media and social networking service owned and operated by American company X Corp.,
the legal successor of Twitter, Inc. Twitter users outside the United States are legally served by the Ireland-based
Twitter International Unlimited Company, which makes these users subject to Irish and European Union data protection laws.
On Twitter users post texts, photos and videos known as 'tweets'. Registered users can tweet, like, 'retweet' tweets,
and direct message (DM) other registered users, while unregistered users only have the ability to view public tweets.
Users interact with Twitter through browser or mobile frontend software, or programmatically via its APIs.
"""
facebook = """
Facebook is an online social media and social networking service owned by American technology giant Meta Platforms.
Created in 2004 by Mark Zuckerberg with fellow Harvard College students and roommates Eduardo Saverin, Andrew McCollum,
Dustin Moskovitz, and Chris Hughes, its name derives from the face book directories often given to American university students.
Membership was initially limited to only Harvard students, gradually expanding to other North American universities and,
since 2006, anyone over 13 years old. As of December 2022, Facebook claimed 2.96 billion monthly active users, and ranked third
worldwide among the most visited websites. It was the most downloaded mobile app of the 2010s. Facebook can be accessed from devices
with Internet connectivity, such as personal computers, tablets and smartphones. After registering, users can create a profile
revealing information about themselves. They can post text, photos and multimedia which are shared with any other users who have
agreed to be their friend' or, with different privacy settings, publicly. Users can also communicate directly with each other with
Messenger, join common-interest groups, and receive notifications on the activities of their Facebook friends and the pages they follow.
"""
tiktok = """
TikTok, and its Chinese counterpart Douyin (Chinese: 抖音; pinyin: Dǒuyīn), is a short-form video hosting service owned by ByteDance.
It hosts user-submitted videos, which can range in duration from 3 seconds to 10 minutes. Since their launches, TikTok and Douyin have
gained global popularity.[6][7] In October 2020, TikTok surpassed 2 billion mobile downloads worldwide. Morning Consult named TikTok the
third-fastest growing brand of 2020, after Zoom and Peacock. Cloudflare ranked TikTok the most popular website of 2021,
surpassing google.com.
"""
instagram = """
Instagram is a photo and video sharing social networking service owned by American company Meta Platforms. The app allows users to
upload media that can be edited with filters and organized by hashtags and geographical tagging. Posts can be shared publicly or
with preapproved followers. Users can browse other users' content by tag and location, view trending content, like photos, and follow
other users to add their content to a personal feed. Instagram was originally distinguished by allowing content to be framed only in a
square (1:1) aspect ratio of 640 pixels to match the display width of the iPhone at the time. In 2015, this restriction was eased with
an increase to 1080 pixels. It also added messaging features, the ability to include multiple images or videos in a single post, and a
Stories feature—similar to its main competitor Snapchat—which allowed users to post their content to a sequential feed, with each post
accessible to others for 24 hours. As of January 2019, Stories is used by 500 million people daily.
"""
documents = [twitter, facebook, tiktok, instagram]
count_vectorizer = CountVectorizer(stop_words="english")
count_vectorizer = CountVectorizer()
sparse_matrix = count_vectorizer.fit_transform(documents)
doc_term_matrix = sparse_matrix.todense()
df = pd.DataFrame(
doc_term_matrix,
columns=count_vectorizer.get_feature_names_out(),
index=["twitter", "facebook", "tiktok", "instagram"],
)
print(df)
print(cosine_similarity(df, df))Before getting to results, it’s good to think about the expected outcomes. Since the same company owns Facebook and Instagram and they’re mostly used to share photos and videos, we can suppose that they are more similar to each other than to other social networks. Twitter might be more similar to Facebook and Instagram than to TikTok, just because of the format of posting, which is quite specific to TikTok. But enough guessing, let’s take a look:
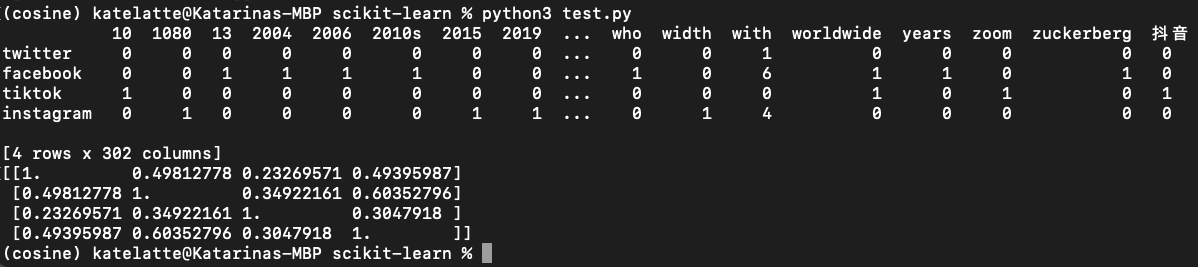
First, there is a matrix of word frequency in all four texts. Cosine similarity is calculated based on that matrix, and, in the end, is also turned into a matrix. Here is how to read the results:
- The first column represents the description of the first social network — Twitter. Every row in the first column represents cosine similarity to all four other social networks. In this case, it means that the cosine similarity of Twitter itself is 1 and that is true since those two texts are the same. That is also the reason why the whole diagonal equals 1 — it represents the cosine similarity of every social network between themselves. The next row in the first column is the cosine similarity of Twitter and Facebook vectors, while the third row is that of Twitter and TikTok vectors. In the end, we have a similarity between Twitter and Instagram vectors. Notice how the similarities of Twitter to Instagram and Facebook are quite close, leading us to the conclusion that Instagram and Facebook descriptions are similar. To check that, see the second column which shows the similarities to the Facebook vector. It goes from Twitter, across Facebook, and TikTok up to the Instagram description. Also notice how the similarity between Facebook and Instagram is quite high, 0.6, while the similarity between Facebook and TikTok is a bit smaller, 0.3.
- Once all columns are read and well interpreted, we can conclude that Facebook and Instagram descriptions (and hence potentially social networks) are the most similar ones. Also, Twitter is more similar to Facebook and Instagram than to TikTok.
Practical use cases of cosine similarity
Cosine similarity is used in various applications, mostly by data scientists, to perform tasks for machine learning, natural language processing, or similar projects. Their applications include:
- Text analysis, which is applied to measure the similarity between documents and offers crucial functionality for search engines and information retrieval systems, as shown in the example.
- Recommendation systems, to recommend similar items based on user preferences or to suggest similar users in social network applications. An example is to recommend the next page on product documentation based on the text similarity found.
- Data clustering, which in machine learning acts as a metric to classify or cluster similar data points, and in that way, it helps make data-driven decisions.
- Semantic similarity, which, when paired with word embedding techniques like Word2Vec, is used to determine the semantic similarity between words or documents.
Cosine similarity in graph databases
Graph databases are popular for how they represent the relationships between different entities, that is, nodes. These relationships are essential in obtaining information about the similarity between nodes in the database. Nodes can hold multi-dimensional data, like feature vectors or descriptions, and cosine similarity can provide an understanding of node relationships beyond mere structural connections.
Whether it's about identifying similar user profiles in a social network, detecting similar patterns in a communication network, or classifying nodes in a semantic network, cosine similarity contributes valuable insights. Combined with a powerful graph database system, such as Memgraph, it gives a better understanding of complex networks. Memgraph is an open-source in-memory graph database built to handle real-time use cases at an enterprise scale. Memgraph supports strongly-consistent ACID transactions and uses the standardized Cypher query language for structuring, manipulating, and exploring data.
To run cosine similarity in Memgraph, you need to install Memgraph with MAGE, Memgraph Advanced Graph Extensions, an open-source repository that contains graph algorithms and modules written by the team behind Memgraph and its users in the form of query modules. One of the query modules implemented is node_similarity. Within that module, procedures to calculate cosine similarity between two vectors and two sets of vectors can be found. Besides that, there are procedures to calculate the Jaccard and overlap similarity.
For example, let’s run the cosine_pairwise procedure from the node_similarity module on a simple example. First, run Memgraph with MAGE using the following Docker command:
```docker run -it -p 7687:7687 -p 7444:7444 memgraph/memgraph-platform````
The Docker image is called Memgraph Platform since it includes the visual user interface of Memgraph Lab, Memgraph database, and MAGE. Exploring data with Memgraph Lab within Docker container will be easier, rather than just using the command line tool or installing Memgraph Lab separately as a Desktop application. Next, load the dataset by running the following queries in the Memgraph Lab Query Execution tab:
CREATE (b:Node {id: 0, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 1, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 2, score: [1.0, 1.0, 1.0]});
CREATE (b:Node {id: 3, score: [1.0, 1.0, 0.0]});
CREATE (b:Node {id: 4, score: [0.0, 1.0, 0.0]});
CREATE (b:Node {id: 5, score: [1.0, 0.0, 1.0]});
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 0}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 1}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 4}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 2}) MERGE (b:Node {id: 5}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 0}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 4}) MERGE (b:Node {id: 1}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 2}) CREATE (a)-[:RELATION]->(b);
MERGE (a:Node {id: 5}) MERGE (b:Node {id: 3}) CREATE (a)-[:RELATION]->(b);If you’re not sure how to do that, refer to the Memgraph Lab user manual.
Every node has a score property, a vector of zeros and ones. Execute the following query to run the cosine_pairwise procedure:
MATCH (m)
WHERE m.id < 3
WITH COLLECT(m) AS nodes1
MATCH (n)
WHERE n.id > 2
WITH COLLECT(n) AS nodes2, nodes1
CALL node_similarity.cosine_pairwise("score", nodes1, nodes2) YIELD node1, node2, similarity AS cosine_similarity
RETURN node1, node2, cosine_similarity;The above query split all nodes into two lists of equal size and used them as arguments of the cosine_pairwise procedure. Here is the result:
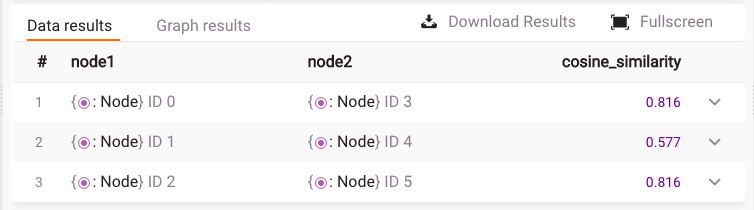
The obtained result calculated cosine similarity based on score properties on nodes. We can see that node 0 is as similar to node 3 as node 2 is similar to node 5. Still similar, but a bit less, is node 1 to node 4.
One of the beauties of graph databases is that there are other popular methods to calculate similarities and, in that way, create recommendation systems. One example of using popular node2vec and link prediction algorithms can be found in our blog post on how to create a docs recommendation system
 .
.
Another interesting example of link prediction with node2vec can be found in how to perform paper recommendations in a physics collaboration network.
Important takeaways
Intuitive interpretation and versatility of the cosine similarity algorithm have found their way into various applications, spanning from text analysis and recommendation systems to complex graph databases. The algorithm's ability to capture the orientation of vectors makes it a robust measure of similarity, especially in high-dimensional spaces.
Python, being a programming language with an abundant set of libraries like scikit-learn, provides data analysts and machine learning enthusiasts with the tools they need to compute cosine similarity with ease. As we increasingly move towards data-driven decision-making, the ability to measure and interpret similarity becomes more crucial than ever. Undoubtedly, cosine similarity will continue to be a valuable tool in data science.
If you want to dive into the world of graph analytics to discover even more about data analysis, sign up for Memgraph’s Graph analytics with Python webinar. For any questions or just a chat about Python, data science, and graphs, join the conversation on our Discord server.