Recommendation System Using Online Node2Vec With Memgraph MAGE

The online node2vec algorithm learns and updates temporal node embeddings on the fly for tracking and measuring node similarity over time in graph streams.

Our little magician Memgraph MAGE has recently received one more spell - the Online Node2Vec algorithm. Since he is still too scared to use it, you, as a brave spirit, will step up and use it on a real challenge to show MAGE how it's done. This challenge includes building an Online Recommendation System using k-means clustering and the newborn spell - Online Node2Vec algorithm.

Prerequisites

To complete this tutorial, you will need:

• An installation of Memgraph Advanced Graph Extensions (MAGE)
• An installation of Memgraph Lab or usage of Memgraph's command-line tool, mgconsole, which is installed together with Memgraph.

Note: In short, you could have one of the following setups:

1. Memgraph installed (not the Docker version), and Memgraph MAGE built from source
2. The Memgraph MAGE Docker image
3. The Memgraph Docker image, but you have to additionally copy the MAGE directory inside the container, run python build and copy the created mage/dist to /usr/lib/memgraph/query_modules so Memgraph can access it.

To check that you have everything ready for the next steps, use the following command in mgconsole or Memgraph Lab:

CALL node2vec_online.help() YIELD *;

Graph

You will use the spell on the High-energy physics citation network. The already processed dataset contains 395 papers - nodes and 1106 citations - edges. If a paper i cites paper j, the graph contains a directed edge from i to j.

Below is the graph schema:

There is only one type of node in our graph schema. MAGE is happy to hear this kind of news since he believes that this way, his spell will give you the best results.

Before importing the dataset, MAGE wants you to read the instructions about the spell to learn how to use it properly.

Online Node2Vec

In the MAGE instructions, there is a note that researchers have shown how the Node2Vec Online spell creates similar embeddings for two nodes (e.g. v and u) if there is an option to reach one node from the other across edges that appeared recently. In other words, the embedding of a node v should be more similar to the embedding of node u if we can reach u by taking steps backward to node v across edges that appeared before the previous one. These steps backward from one node to the other form a temporal walk. It is temporal since it depends on when the edge appeared in the graph.

To make two nodes more similar and to create these temporal walks, the Node2Vec Online spell uses the StreamWalk updater and Word2Vec learner.

StreamWalk updater is a machine for sampling temporal walks. A sampling of the walk is done in a backward fashion because we look only at the incoming edges of the node. Since one node can have multiple incoming edges, when sampling a walk, StreamWalk updater uses probabilities to determine which incoming edge of the node it will take next, and that way leading to a new node. These probabilities are computed after the edge arrives and before temporal walk sampling. Probability represents a sum over all temporal walks z ending in node v using edges arriving no later than the latest one of already sampled ones in the temporal walk. When the algorithm decides which edge to take next for temporal walk creation, it uses these computed weights (probabilities). Every time a new edge appears in the graph, these probabilities are updated just for two nodes of a new edge.

After walks sampling, Word2Vec learner uses these prepared temporal walks to make node embeddings more similar using the gensim Word2Vec module. These sampled walks are given as sentences to the gensim Word2Vec module, which then optimizes for the similarity of the node embeddings in the walk with stochastic gradient descent using a skip-gram model or continuous-bag-of-words (CBOW).

Note: this implementation contains the code related to the research of Ferenc Béres, Róbert Pálovics, Domokos Miklós Kelen and András A. Benczúr

Node2Vec Online setup

From MAGE's instructions, you see now a piece of advice to use Memgraph Triggers for this spell to work. You can create a trigger that fires up on edge creation. Every time there is a new edge which we add in the graph, trigger fires and calls Node2Vec Online algorithm to update node embeddings.

To create the trigger, you can use the following command in Memgraph Lab or mgconsole:

CREATE TRIGGER trigger ON --> CREATE BEFORE COMMIT
EXECUTE CALL node2vec_online.update(createdEdges) YIELD *;

Before you start with importing the dataset, there is a big message on MAGE's instructions not to forget to set parameters for StreamWalk updater and Word2Vec learner.

StreamWalk updater uses the following parameters:

• half_life: half-life [seconds], used in the temporal walk probability calculation
• max_length: maximum length of the sampled temporal random walks
• beta: damping factor for long paths
• cutoff: temporal cutoff in seconds to exclude very distant past
• sampled_walks: number of sampled walks for each edge update
• full_walks: return every node of the sampled walk (True) or only the endpoints of the walk (False)

All these parameters are for temporal walk sampling. And you can set now the parameters with the following command in Memgraph Lab or mgconsole:

CALL node2vec_online.set_streamwalk_updater(7200, 5, 0.9, 604800, 5, True)
YIELD *;

Word2Vec learner uses the following parameters:

• embedding_dimension: number of dimensions in the representation of the embedding vector
• learning_rate: learning rate
• skip_gram: use skip-gram model
• negative_rate: negative rate for skip-gram model
• threads: maximum number of threads for parallelization

These parameters are mostly used in the skip-gram model. You can set the parameters with the following command in Memgraph Lab or mgconsole:

CALL node2vec_online.set_word2vec_learner(4,0.01,True,10) YIELD *;

Loading a dataset

Now, Memgraph and Node2Vec online are ready, and you can download and import the prepared dataset through your terminal:

mgconsole --use-ssl=false < graph.cypherl

After you execute this command, the trigger will fire upon every new edge that appears in the graph. This will take around 1 minute to calculate embeddings. Now you can add new edges and node2vec_online query module will update the embeddings and it will be ready for usage.

Recommendation system

Here you will build a recommendation system and show MAGE how it is done.

Before you continue, if you call this command, you should see that embeddings are ready. Again, execute the query in Memgraph Lab or mgconsole:

CALL node2vec_online.get() YIELD node, embedding
RETURN count(embedding) as embeddings_count;

To create a recommendation engine, GitHub is offering you help. He heard that you want to impress MAGE and has some code already prepared here. You can trust him since he is also part of Memgraph. Download a code and be ready to spin it up.

The recommendation engine will base on k-means from scikit-learn pacakge.

The k-means algorithm clusters data by trying to separate samples in n groups of equal variance, minimizing a criterion known as the inertia or within-cluster sum-of-squares. This algorithm requires the number of clusters to be specified. It scales well to a large number of samples and has been used across a large range of application areas in many different fields.

In our procedure, we will first get embeddings from the node2vec_online module. After that, using the elbow method for k-means inertia will give you the best k value, which represents the number of clusters. GitHub, which offered you help, recommends you to use 5 clusters, but you can try out different numbers of clusters.

You can visualize k-means inertia using this command:

python3 recommender.py visualize

Here we are using k-means since we want to find which embeddings are close to each other in vector space, which would give us papers (nodes) that are similar in physics.

After finding groups of similar papers, we are ready to get papers that are most similar by running the command:

python3 recommender.py similarities --n_clusters=5 --top_n_sim=5

After we get the results, there is one example of 99.7% similarity.

This is exaggerated a lot on one side since we can't be sure just from the graph that these two papers are this similar, but from the graph structure presented later, it is expected that these two nodes have high similarity. From the description, we can see that papers are similar as they talk about similar topics. 99.7% is still a lot, but the algorithm works well! MAGE is impressed.

                   id: 9606040                                                                    id: 9610195                                                                       STATS
       title: Mirror Symmetry is T-Duality                              title: Unification of M- and F- Theory Calabi-Yau Fourfold Vacua
                                                                                                                                                                              similarity:0.9973


It is argued that every Calabi-Yau manifold  X  wi                             We consider splitting type phase transitions betwe
th a mirror  Y  admits a family of supersymmetric                              en Calabi-Yau fourfolds. These transitions general
toroidal 3-cycles. Moreover the moduli space of su                             ize previously known types of conifold transitions
ch cycles together with their flat connections is                               between threefolds. Similar to conifold configura
precisely the space  Y . The mirror transformation                             tions the singular varieties mediating the transit
 is equivalent to T-duality on the 3-cycles. The g                             ions between fourfolds connect moduli spaces of di
eometry of moduli space is addressed in a general                              fferent dimensions, describing ground states in M-
    framework. Several examples are discussed.                                  and F-theory with different numbers of massless m
                                                                               odes as well as different numbers of cycles to wra
                                                                               p various p-branes around. The web of Calabi-Yau f
                                                                               ourfolds obtained in this way contains the class o
                                                                               f all complete intersection manifolds embedded in
                                                                               products of ordinary projective spaces, but extend
                                                                               s also to weighted configurations. It follows from
                                                                                this that for some of the fourfold transitions va
                                                                               cua with vanishing superpotential are connected to
                                                                                   ground states with nonzero superpotential.
--------------------------------------------------                             --------------------------------------------------                             --------------------------------------------------

Using Memgraph Lab, we can now visualize some of the data:

MATCH connection = (a:Paper)-[*bfs..10 (e, n | 'Paper' IN labels(n))]-(b:Paper)
WHERE
    (a.id = "9610195" AND b.id = "9606040")
    OR
    (a.id="9606040" and b.id="9610195")
RETURN connection;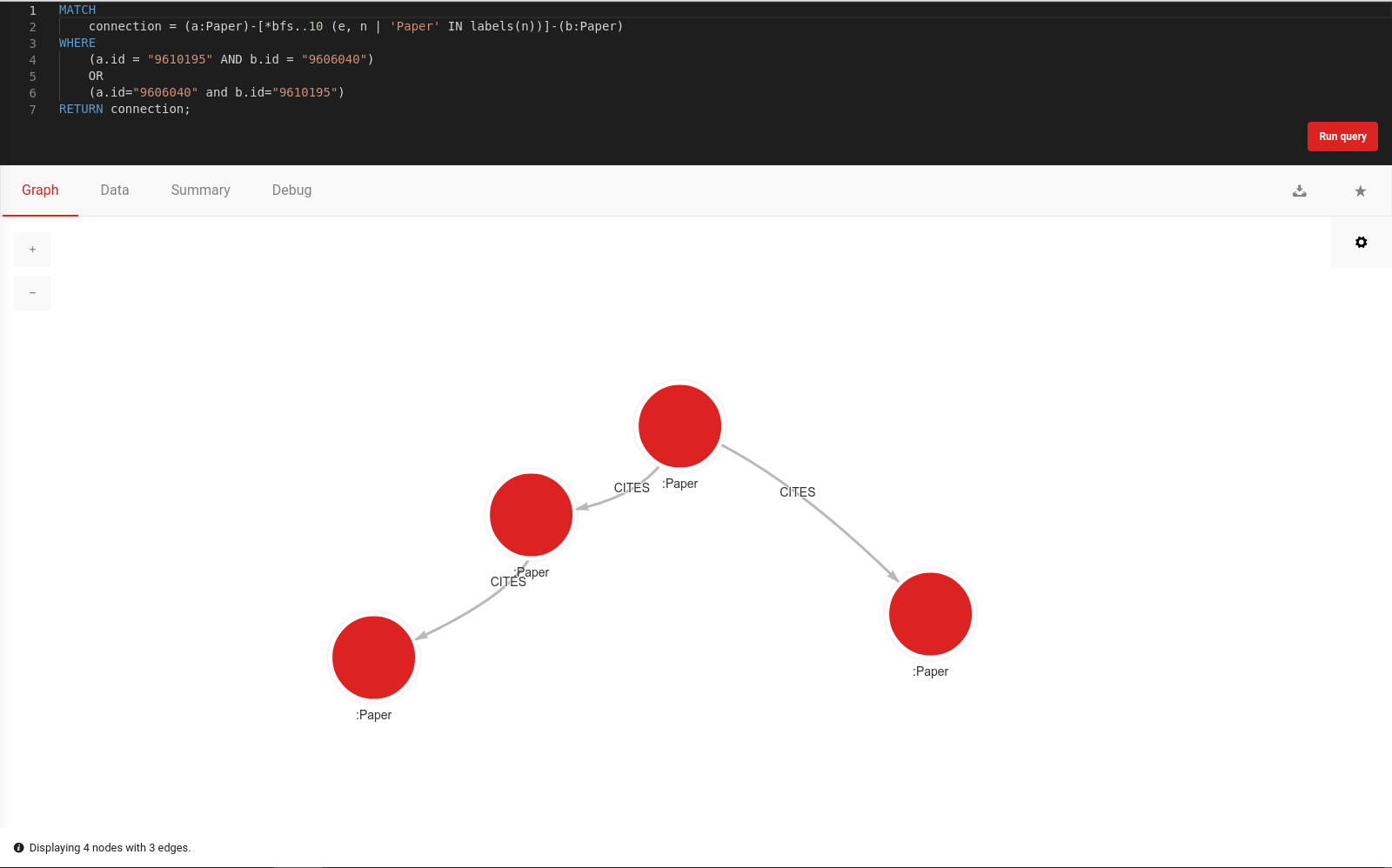

Conclusion

Finding similar papers just from the graph structure is a complicated task, but the results are very promising. You can take similar steps in different domains. The main advantage of this algorithm is that it works completely online, which is a great functionality in today's world when more and more data is event-driven.

MAGE is a versatile open-source library containing standard graph algorithms that can help you analyze graph networks. While many graph libraries out there are great for performing graph computations, using MAGE and Memgraph provides you with additional benefits like persistent data storage and many other graph analytics capabilities.

If you found this tutorial beneficial, you should try out the other algorithms included in the MAGE library.

Finally, if you are working on your query module and would like to share it with other developers, take a look at the contributing guidelines. We would be more than happy to provide feedback and add the module to the MAGE repository.

References:

[1] F. Béres, D. M. Kelen, R. Pálovics and A. A. Benczúr. Node embeddings in dynamic graphs. 2019.