Dynamic PageRank on Streaming Data
Introduction
PageRank is one of those iconic algorithms that have changed the world of technology forever. You probably know Google's story - after designing a brilliant algorithm that is able to measure the influence of a webpage simply by looking at who has a link toward the targeted webpage, Google has changed the course of history within a web-browsing niche.
Where can PageRank be used?
PageRank can be used as an influence measurement in many different applications when working with highly interconnected data. For example, one can wonder who is an influential individual in the connected data of social network interactions. Others might want to investigate transactions made by a particular individual in some financial data warehouses. Having an influence measurement, in that case, can lead toward finding who is collaborating with a suspicious number of entities, which could be interpreted as fraudulent behavior. Finally, an extremely intersected internet network may require influence measurement to pinpoint the specific place where a data transfer bottleneck could occur.
All these examples have one thing in common: they can be solved/investigated with proper influence measurement information. Organizing data as connected entities within a graph opens up the possibility of using graph algorithms that are specifically designed for such problems. This is what the world's largest companies have been doing for years. However, the real world demands solving problems that are further ahead in the process of reaching the goal.
Large and constantly evolving data quickly makes common approaches obscure. While going through the following sections, think about your data, question yourself whether it is large or not, and whether it evolves with time or it's static. If you have large and dynamic data, this article can help you dive into building an influence measurement that constantly updates whenever new data is available.
How to use PageRank on dynamic data?
An obvious and trivial solution to the previous problem would be: whenever a new data point or connection comes into our platform, simply recalculate the influence measurement with the PageRank algorithm. This is very simple, and it works. However, the story changes over time when your business becomes more popular. You begin to have more work and therefore datapoints keep coming at a faster pace, accumulated data keeps rising in size and your algorithm fails to deliver valuable information efficiently.
To prevent that from happening, the next section will describe the method for incrementally updating PageRank measurements whenever a new data point hits the platform.
Imagine a case where data is ingested via streaming, and you demand an almost real-time answer to what is the influence of some entity.
Incremental PageRank on streaming data
I am going to describe the algorithm with the most simple and yet genius idea of how to update influence/ranking when new information is added into the system. The work from Twitter employees described in "Fast Incremental and Personalized PageRank" by Bahmani et al. can be simply put like this:
- Approximatively calculate the influence measurement on your current, static data.
- When a new connection/data point comes into the system, recalculate measurement only on data that is affected by the update.
The first one is trivial. There are numerous techniques to empower the PageRank algorithm on static data. One of them is approximative.
Approximative PageRank
Intuitively, a PageRank is the probability to end up in a certain node starting from a randomly picked one. Implementing that exact idea is going to lead toward the approximative solution to the problem. If we sample R different random walks of average length 1/ε, where ε notes the probability of finishing a random walk, we have enough information to approximate centrality/influence.
Now, for a node v, let's introduce variable Xᵥ that denotes the number of times that v is stored in some random walk. If n is a number of total nodes, by the definition that was mentioned previously, PageRank can be approximated with the next formula:
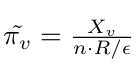
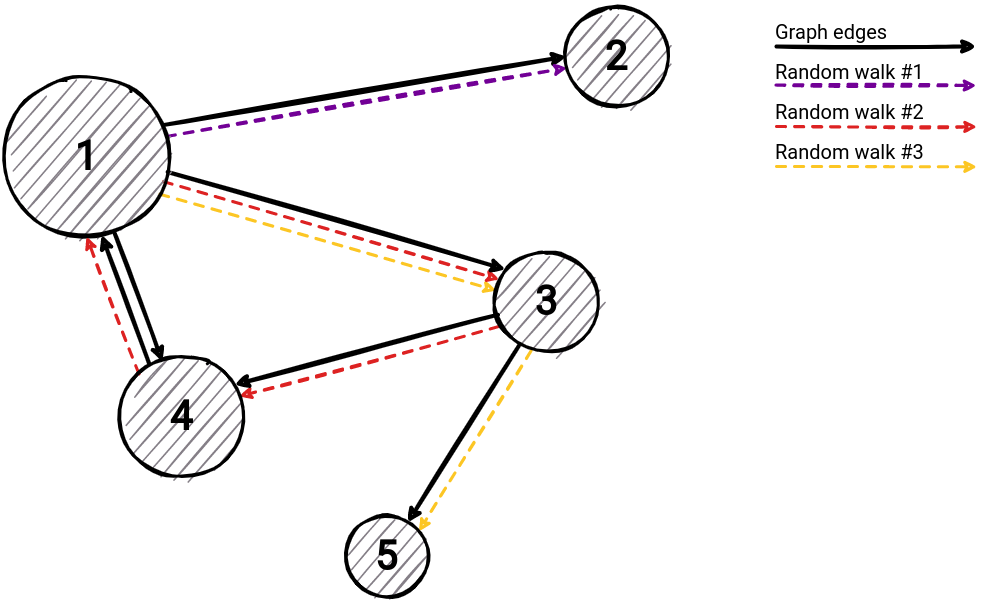
Incremental update
When saying, "recalculate measurement only on data which is affected by the update" one wonders what specific data points should be updated once new data hits the system. We can think about it like this: after creating a connection, or a new data point, we are going to trigger an update on PageRank values for each node.
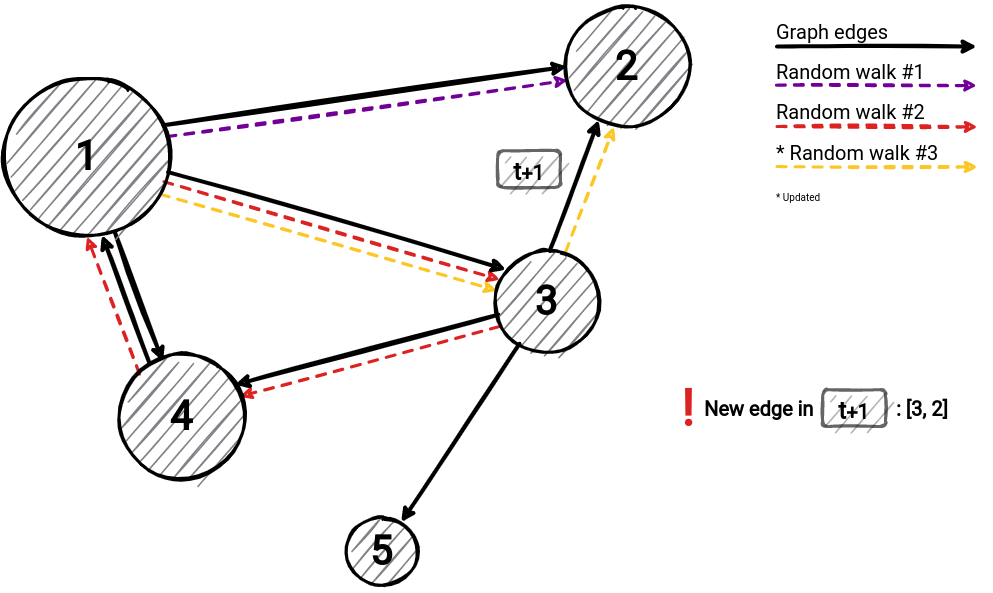
Calculation of parameters depends on previously calculated walks, therefore we need to store them beforehand. After we recalculate routes, we can easily derive new PageRank values from the formula above. Walks that need to be changed are affected by new graph entities. If a connection is added, all walks that are going through the connection's nodes need to be changed (the image below shows how walk #3 updates once a new edge arrives). As mentioned, after these changes, the calculation of PageRank is trivial by reusing the stored information and formula above.
Conclusion
The idea of this article is to describe how a smart algorithm can spare a large number of computations and deliver valuable insights into data faster than before. With the current progress and rise in streaming data, such insight can solve troubles for a huge amount of companies.
Our team of engineers is currently tackling the problem of graph analytics algorithms on real-time data. If you want to discuss how to apply online/streaming algorithms on connected data, feel free to join our Discord server and message us.
MAGE shares his wisdom on a Twitter channel. Get to know him better by following him 🐦

Last but not least, check out MAGE and don't hesitate to give a star ⭐ or contribute with new ideas.