How to Find All Weighted Shortest Paths Between Nodes and Do It Fast

Many graph use cases rely on finding the shortest path between nodes. When the weight of a path is of no concern, the simplest and best algorithms are Breadth-First Search and Depth-First Search, both of which have a time complexity of O(V + E), where V is the number of vertices and E is the number of edges. On the other hand, on weighted graphs without any negative weights, the algorithm of choice is the Dijkstra algorithm, which, when optimized, has a time complexity of O(E + VlogV). Other, more specific algorithms exist. When faced with negative weights, you can use the Bellman-Ford algorithm which has a complexity of O(VE). Johnson’s algorithm utilizes Bellman-Ford to find all-pair shortest paths. Another all-pairs algorithm is the Floyd Warshall, which, compared to Johnson’s works better for dense graphs.

These algorithms can also be modified in different ways. One of our customers wanted to find all weighted shortest paths, meaning if there are multiple shortest paths of the same length, Memgraph would return them all. Since Memgraph was still not capable of that, we decided to roll up our sleeves and make it happen.

Finding the best architecture within MAGE

Our initial idea was to create a new query module within the MAGE library because query modules have a better tradeoff between development time and performance compared to built-in algorithms. With Memgraph’s C API, anyone can create their own custom query modules using C/C++ for communication with the data in the database. There is also a Python wrapper for the C API so if you are a Python enthusiast with an idea for an algorithm, you can develop it yourself.

In our first iteration of the All Shortest Path algorithm, we used a standard Dijkstra algorithm to run once over each source node. We used the OpenMP library to parallelize this action:

#pragma omp parallel for
   for (std::size_t i = 0; i < sources_size; ++i) {
     auto source = sources[i];
/*
Dijkstra's algorithm for source node.
*/

Once the algorithm finds a path to the target node, the path needs to be listed as one of the results. This is done by entering a critical section using #pragma omp critical, which communicates with the API.

Using the std::chrono library and the functions below, we timed the algorithm and found that that critical section and communication over C API was taking up more than 75% of the runtime.

inline std::chrono::time_point<std::chrono::high_resolution_clock> StartTimer() {
 return std::chrono::high_resolution_clock::now();
}
inline double EndTimer(std::chrono::time_point<std::chrono::high_resolution_clock> start) {
 return ((std::chrono::duration<double, std::milli>)(std::chrono::high_resolution_clock::now() - start)).count();
}

To improve the runtime, we thought about storing all the paths the Dijkstra algorithm finds at once, after the parallel section. But in some cases the number of paths can be so large that storing them would take up too much memory, so to compensate, we decided on a different approach - to store the parents of every node in a map:

std::unordered_map<std::uint64_t, std::vector<std::pair<std::uint64_t, std::uint64_t>>> next_edges_;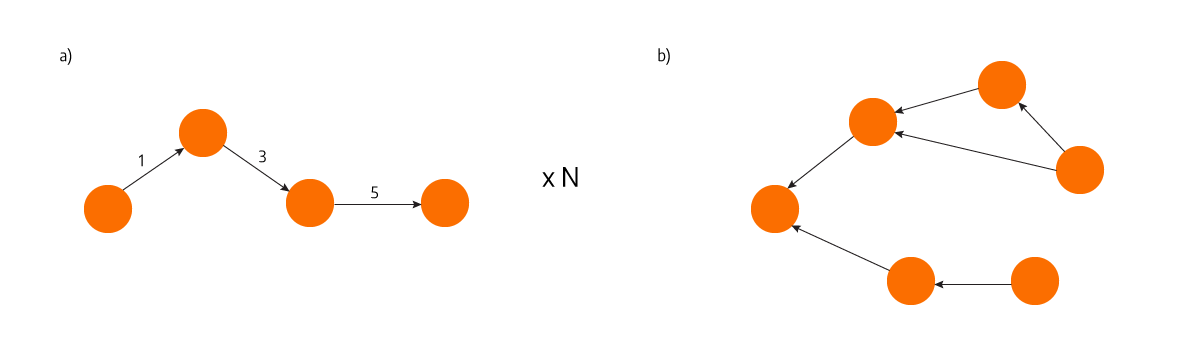

This picture shows the difference between a) storing N paths separately and b) storing just the parents of each node in a single map.

It’s important to point out that the values in the map are vectors, so each node can have multiple parents, which consequently allows multiple paths of the same length. The parent nodes saved in the map thus make an unweighted graph and the DFS algorithm can construct paths out of it without noticeably slowing down the runtime because it’s so much less time-consuming than the Dijkstra algorithm.

To speed up the algorithm even more, we exploited the fact that Dijkstra uses a priority queue to determine the order of nodes to visit, and is, therefore, optimal to use a Fibonacci heap priority queue. As opposed to the standard C++ library priority queue’s max heap, the Fibonacci heap uses O(1) amortized time to update a priority of an item, which is a common operation in Dijkstra whenever it reaches a visited node with a lower path length.

These changes improved the execution of the Dijkstra algorithm, making the All Shortest Path algorithm 20% faster, but we were not even close to achieving the wanted speed. We abandoned the idea of creating a new MAGE query module and started working on a core implementation instead.

Integrating the algorithm into Memgraph core to optimize path ingestion

Memgraph’s core has a query plan consisting of cursors in a pipeline connected to their neighbors, as shown in the diagram above. The new All Shortest Paths built-in algorithm is implemented as a cursor. The cursors communicate using Pull methods (indicated by the arrows), which return true to indicate that the next cursor in the pipeline can keep pulling, or false to indicate that the pipeline is exhausted.

ExpandAllShortestPathsCursor calls Pull from its input cursor Filter, receiving a single node that needs to be expanded upon. For each call of the ASP algorithm, it should return a single path to be able to work as a cursor, but Dijkstra needs to run through the whole graph first to be sure that there is no shorter path than this one.

After Dijkstra, the DFS, which is used to construct paths, takes over. DFS is designed so that it can stop after every path that is returned by using traversal_stack_, which indicates the traversal level it is currently on, allowing the DFS to resume without needing to rerun Dijkstra the next time Pull is called.

One of the issues we faced was implementing an upper bound, a maximum depth of search for the algorithm. At first, it seemed straightforward, just stopping the algorithm from going further when it reached a certain depth, but there were edge cases that would not adhere to this logic. For example, if there are two paths between a pair of nodes, one of which is shorter, but visits more nodes, and the other that has more weight, but has less depth, if the upper bound eliminated the first path, the Dijkstra algorithm would not return the second path, since it would not expand upon the node state with more weight. For this reason, we modified the next_edges_ key to include depth:

unordered_map<std::pair<VertexAccessor, int64_t>, utils::pmr::list<DirectedEdge>, AspStateHash> next_edges_;

This allowed us to differentiate states of visited relationships. When the upper_bound is not set, the algorithm ignores the depth so that it does not slow down the algorithm unnecessarily by visiting nodes in non-shortest paths.

Using the algorithm

The algorithm was made to be used in the same manner as Memgraph’s Weighted Shortest Path algorithm and boils down to calling [*ALLSHORTEST (r, n | r.weight)] where r and n define the current expansion relationship and node respectively.

To return all shortest paths between two nodes, use the following query:

MATCH path=(n {id: 0})-[Type *ALLSHORTEST (r, n | r.weight)]-(m {id: 5})
RETURN path;

To return the total weight along with each path, define the name used for the weight:

MATCH path=(n {id: 0})-[Type *ALLSHORTEST (r, n | r.weight) total_weight]-(m {id: 5})
RETURN path, total_weight;

You can also set the upper bound, and filter the expansion based on property values. To learn how to do that, head on to Memgraph’s documentation.

Conclusion

The best algorithm for the job depends on the type of graph and the needs of the application, as we pointed out while listing the differences between algorithms for finding the shortest paths. In this under-the-hood look at the All Shortest Paths algorithm we’ve given you a sneak peek at the development process of one of our built-in algorithms, the bumps we faced, the analysis of the runtime we made, and the problems we solved to make it work with Memgraph so our users can get better insight into their data.

Memgraph currently has built-in support for BFS, DFS, WSHORTEST, and now ALLSHORTEST algorithms. You can check them out in Memgraph’s documentation. But the MAGE library supports many more graph algorithms, written as query modules. And as we already mentioned, by using the C API you can create your own query modules to create algorithms specific to your needs, and even contribute to the MAGE library to share the knowledge with the rest of the graph community. Tell us about your work on our Discord server, we’ll be happy to hear about it or provide any help.