Introduction to Node Embedding
Introduction
In this article, we will try to provide an explanation to the following questions:
- What are node embeddings?
- How to generate node embeddings?
- When can we even use node embeddings?
This is a lot to cover in one article, but let's give it our best. Any prior knowledge of graphs or machine learning is not necessary, just a bonus. First, let's start with graphs. 🚀
Graphs
Graphs consist of nodes and edges - connections between the nodes.
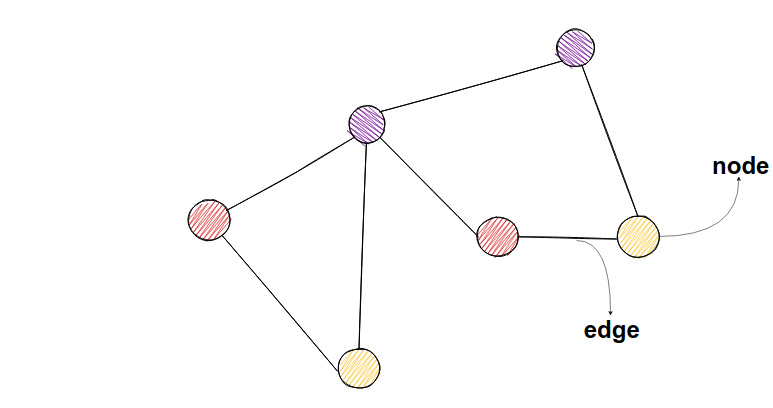
In social networks, nodes could represent users, and links between them could represent friendships.
One interesting thing you can do with graphs is to predict which tweets on Twitter are from bots, and which are from organic users. How would we achieve that? Well, stick around and you will get an idea of how it can be done.
What are node embeddings?
So what does embedding mean, and why is it useful?
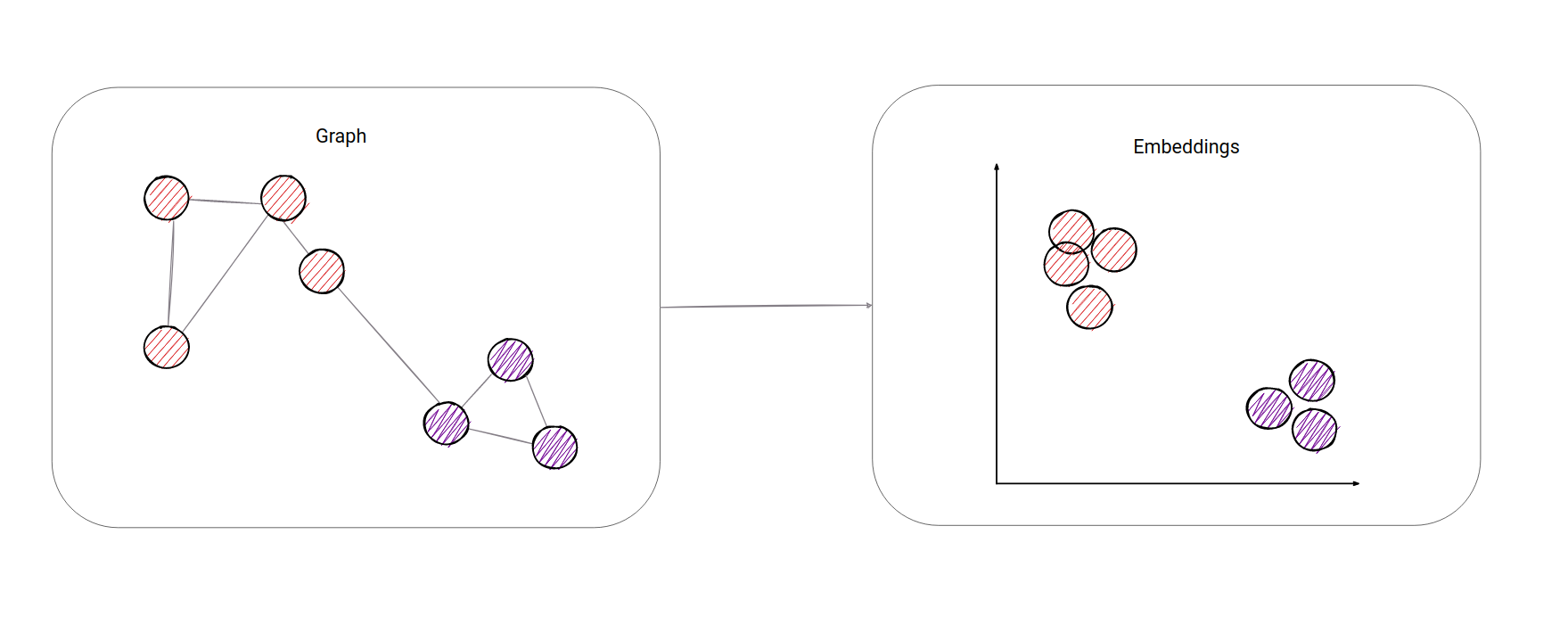
To embed, per the English dictionary, means to fix something in a substance or solid object. With graphs, it would mean to map the whole graph in N-dimensional space. Take a look at the example below. In this example, we mapped all the nodes in 2-dimensional space. Now, it should be obvious we have two clusters (or communities) in the graph. For us humans, it is easier to identify clusters in 2-dimensional space. In this example, it is also easy to spot clusters just from the graph layout, but imagine the graph having 1000 nodes - things aren't as straightforward anymore.
Furthermore, for a computer, it is easier to work with node embeddings (vectors of numbers), because it is easier to calculate how similar (close in space) 2 nodes are from embeddings in N-dimensional space than it would be to calculate from a graph only. On the other hand, there is no proper way how we could calculate the closeness of two nodes just from the graph. You could use something like the shortest path algorithm, but that itself is not representative enough. With vectors, it's easier. The most often used metric is called cosine similarity.
Now we have something a computer can work with:
Now we know what embeddings are, but what do we use node embeddings for?
Supervised machine learning is a subset of machine learning where algorithms try to learn from data. Data is represented by input-output pairs, i.e. [2] -> 2, [1] -> 1. Our model tries to learn from data in such a way that it maps inputs to the correct outputs. In our example ([2] -> 2, [1] -> 1) model would try to learn function y=x. Here, it would be pretty easy for the model to learn input-output mapping, but imagine a problem where a lot of different points from input space map to same output value. That's why we can't directly apply a machine learning algorithm to our input-output pairs, but we first need to find a set of informative, discriminating, and independent features amongst input data points. Finding such features is an often difficult task.
In prediction problems on networks, we would need to do the same for the nodes and edges. A typical solution involves hand-engineering domain-specific features based on expert knowledge. Even if one discounts the tedious effort required for feature engineering, such features are usually designed for specific tasks and do not generalize across different prediction tasks.
This sounds like a bad news. 👎
We want our algorithm to be independent of the downstream prediction task and that the representations can be learned in a purely unsupervised way. This is where node embeddings come into place.
We will make our algorithm learn embeddings, and after that, we can apply those embeddings in any of the following applications, one of which is Twitter bot detection. Let's dig in.
How to generate node embeddings?
Researches have divided these methods into three broad categories:
- Factorization based
- Random Walk based
- Deep Learning based
1. Factorization based
Factorization based algorithms represent the connections between nodes in the form of a matrix and factorize this matrix to obtain the embedding. In one such method called Local Linear Embedding, there is the assumption that every node is a linear combination of its neighbors, so the algorithm tries to represent the embedding of every node as a linear combination of its neighbors' embeddings. It is like the example from high school where you need to represent one vector as a linear combination of other two vectors. Only here, you can have multiple vectors, and they are much more complex.
2. Random walks
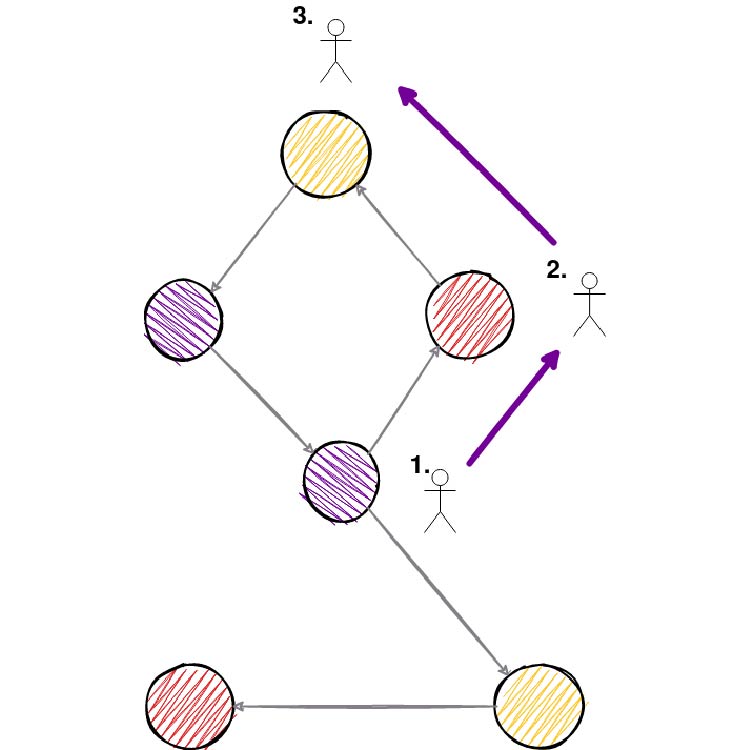
Random walk based methods use a walk approach to generate (sample) network neighborhoods for nodes. For every node, we would generate its network neighborhood by choosing in some way (depends on the method, can be random or it can include probabilities) the next node of our walk. You can take a look at the picture below of how it would look like.
The maximum walk length is determined before this process of walk sampling, and for every node, we generate N random walks. By doing so, we have created a network neighborhood of a node. And now our goal would be to make a node as similar as possible to nodes in its network neighborhood.
Again with this boring question, but why do this?
Turns out this process was proven to be very good in another area called natural language processing dealing with words/documents where you want to find similar words. For example, words "intelligent" and "smart" should be similar words. This method in natural language processing is called word2vec. Words that appear in a similar context (words before or after that word), should be similar. Thankfully, the same applies to nodes. Nodes that appear in a similar context (sampled walks) should be similar. Our process of walk sampling is used to create a dataset on which we will try to make node embeddings as similar as possible. 🤯 And that is it. The dataset in word2vec methods is every sentence of a document, and analogously for us, it is every sampled graph random walk.
3. Deep learning
The growing research on deep learning has led to the usage of deep neural network-based methods applied to graphs. With deep learning, it is easier to model non-linear structures, so deep autoencoders have been used for dimensionality reduction. A few popular methods from this area are called Structural Deep Network Embedding (SDNE) and Deep Neural Networks for Learning Graph Representations (DNGR) so feel free to check them out.
Where can node embeddings be applied?
We know that graphs occur naturally in various real-world scenarios such as social networks (social sciences), word co-occurrence networks (linguistics), interaction networks (i.e. Protein-Protein interactions in biology), and so on. Modeling the interactions between entities as graphs have enabled researchers to understand the various networks in a systematic manner. For example, social networks have been used for applications like friendship or content recommendations, as well as for advertisement.
But how are researchers modeling such interactions? You may already have the answer.
By embedding a large graph in low dimensional space (a.k.a. node embeddings). Embeddings have recently attracted significant interest due to their wide applications in areas such as graph visualization, link prediction, clustering, and node classification. It has been demonstrated that graph embedding is superior to alternatives in many supervised learning tasks, such as node classification, link prediction, and graph reconstruction. Here is a chronological list of research papers where you can check them out:
- Distributed large-scale natural graph factorization, Ahmed et al., 2013;
- DeepWalk: online learning of social representations, Perozzi et al., 2014;
- Deep Neural Networks for Learning Graph Representations, Cao, et al., 2015;
- LINE: Large-scale Information Network Embedding, Tang, et al., 2015;
- node2vec: Scalable Feature Learning for Networks, Grover and Leskovec, 2016;
- Asymmetric Transitivity Preserving Graph Embedding, Ou et al., 2016.
Node classification
Node classification aims to determine the label of nodes (a.k.a. vertices) based on other labeled nodes and the topology of the network. Often in networks, only a fraction of nodes are labeled. In social networks, labels may indicate interests, beliefs, or demographics, whereas the labels of entities in biology networks may be based on functionality. For example, we have some data where researchers have painstakingly worked out the functional role of specific proteins in their system of interest and characterized details of their interaction partners and the pathways in which they function. But still, a lot of them haven't yet been worked out completely. With embeddings, we could try to predict missing labels with high precision.
Link prediction
Link prediction refers to the task of predicting missing links or links that are likely to occur in the future. For example in the Protein-Protein network, where verifying the existence of links between nodes that are proteins requires costly experimental tests, link prediction might save you a lot of money so that you check only where you have a higher chance to guess correctly.
Clustering
Clustering is used to find subsets of similar nodes and group them; finally, visualization helps in providing insights into the structure of the network.
So back to our bot case. One assumption could be made that bots have a small number of links to real users, because who would want to be friends with them, but they have a lot of links between them so that they appear as real users. Graph clustering or community detection come in place here. We want to find those clusters and remove bot users. This can be done with node embeddings, especially dynamic node embeddings, where interactions are made every second.
There is a cool article The Rise of Social Bots in which you can read how bots are used to affect and possibly manipulate the online debate about vaccination policy.
Conclusion
Phew. There was a lot to cover, but we succeeded somehow! Good job if you stayed with me until here! ❤️. Now, after we have covered the theory, you can check out some implementations of node embedding algorithms, for static and dynamic graphs.
Our team of engineers is currently tackling the problem of graph analytics algorithms on real-time data. If you want to discuss how to apply online/streaming algorithms on connected data, feel free to join our Discord server and message us.
MAGE shares his wisdom on a Twitter channel. Get to know him better by following him 🐦

Last but not least, check out MAGE and don't hesitate to give a star ⭐ or contribute with new ideas.